Question

在直角△ABC中，∠BCA=90°，CA=CB=1，设

AP

=λ

AB

，

CQ

=λ

CB

（λ∈R），则

CP

•

AQ

的最小值为（　　）

• A、-

  5

  2

• B、-

  5

  4

• C、-

  3

  4

• D、-

  3

  2

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：把三角形放入直角坐标系中，求出相关点的坐标，利用已知条件即可求出λ的取值范围．

解答： 解：∵直角△ABC中，∠BCA=90°，CA=CB=1，
∴以C为坐标原点CA所在直线为x轴，CB所在直线为y轴，如图：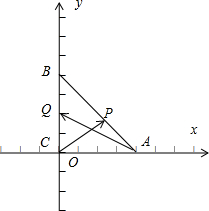
C（0，0），A（1，0），B（0，1），
∵

AP

=λ

AB

，

CQ

=λ

CB

（λ∈R），∴P（1-λ，λ），Q（0，λ）；
∴

CP

=（1-λ，λ），

AQ

=（-1，λ）；
∴

CP

•

AQ

=（1-λ）•（-1）+λ•λ=λ²+λ-1=(λ+

1

2

)2-

5

4

≥-

5

4

，
当λ=-

1

2

时，“=”成立；
∴则

CP

•

AQ

的最小值为-

5

4

．
故选：B．

点评：本题考查了平面向量的应用问题，解题时应根据题意，建立适当地坐标系，利用向量的坐标运算进行计算，是中档题．