题目内容
已知D是等腰△ABC的边BC的中点，AB=AC，PC⊥平面ABC，求证：AD⊥平面PBC．
考点：直线与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：由线面垂直的性质，得到PC⊥AD，再由等腰三角形的性质得到AD⊥BC，再由线面垂直的判定，即可得证．
解答：
证明：∵PC⊥平面ABC，AD?平面ABC，
∴PC⊥AD，
∵D是等腰△ABC的边BC的中点，AB=AC，
∴AD⊥BC，
∵BC∩PC=C，
∴AD⊥平面PBC．
证明：∵PC⊥平面ABC，AD?平面ABC，∴PC⊥AD，
∵D是等腰△ABC的边BC的中点，AB=AC，
∴AD⊥BC，
∵BC∩PC=C，
∴AD⊥平面PBC．
点评：本题考查直线与平面垂直的性质和判定，考查推理能力，属于基础题．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
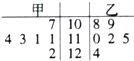某质检机构检测某产品的质量是否合格，在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品，称其质量（单位：克），分别记录抽查数据，获得质量数据茎叶图（如图）．