题目内容
已知抛物线x2=8(y+8)与y轴交点为M,动点P,Q在抛物线上滑动,且
•
=0
(1)求PQ中点R的轨迹方程W;
(2)点A,B,C,D在W上,A,D关于y轴对称,过点D作切线l,且BC与l平行,点D到AB,AC的距离为d1,d2,且d1+d2=
|AD|,若△ABC的面积S=48,求点A的坐标.
| MP |
| MQ |
(1)求PQ中点R的轨迹方程W;
(2)点A,B,C,D在W上,A,D关于y轴对称,过点D作切线l,且BC与l平行,点D到AB,AC的距离为d1,d2,且d1+d2=
| 2 |
考点:直线与圆锥曲线的关系,平面向量数量积的运算,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设为k,设PQ的中点R(x,y),求出P,Q的坐标,继而得到PQ中点R的轨迹方程W.
(2)利用点A的坐标表示弦长|AC|、|AB|,进而利用面积即可得出坐标,
(2)利用点A的坐标表示弦长|AC|、|AB|,进而利用面积即可得出坐标,
解答:
解:(1)显然直线MP的斜率存在且不为0,设为k,设PQ的中点R(x,y),
∴直线MP:y=kx-8与x2=8(y+8)联立解得:P(8k,8k2-8),
同理:Q(-
,
-8),
∴PQ的中点R(4k-
,4k2+
-8),
∴
∴轨迹方程:x2=4y,
(2)由y=
x2得y′=
x,
设D(x0,
x02),C(x1,
x12),B(x2,
x22)则A((-x0,
x02),
∴KBC=
( x1+x2)=
x0,
∴x1+x2=2x0,
∴kAC=
(x1-x0)
又KAB=
(x0-x1)
∴kAC=-kAB,
∴∠DAC=∠DAB,
∴d1=d2,
又d1+d2=
AD得sin∠DAC=
,
∴∠DAC=∠DAB=45°,故△ABC是直角三角形.
设AB:y-
x02=-(x+x0),与抛物线联立得:B( x0-4,
(x0-4)2)
同理:C( x0+4,
(x0+4)2)
∴|AB|=
|x0-4-(-x0)|=
|2x0-4|,
同理:|AC|=
|2x0+4|,
∴S△ABC=
|AB||AC|=48,代入得:A(4,4)或(-4,4).
∴直线MP:y=kx-8与x2=8(y+8)联立解得:P(8k,8k2-8),
同理:Q(-
| 8 |
| k |
| 8 |
| k2 |
∴PQ的中点R(4k-
| 4 |
| k |
| 4 |
| k2 |
∴
|
∴轨迹方程:x2=4y,
(2)由y=
| 1 |
| 4 |
| 1 |
| 2 |
设D(x0,
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴KBC=
| 1 |
| 4 |
| 1 |
| 2 |
∴x1+x2=2x0,
∴kAC=
| 1 |
| 4 |
又KAB=
| 1 |
| 4 |
∴kAC=-kAB,
∴∠DAC=∠DAB,
∴d1=d2,
又d1+d2=
| 2 |
| ||
| 2 |
∴∠DAC=∠DAB=45°,故△ABC是直角三角形.
设AB:y-
| 1 |
| 4 |
| 1 |
| 4 |
同理:C( x0+4,
| 1 |
| 4 |
∴|AB|=
| 2 |
| 2 |
同理:|AC|=
| 2 |
∴S△ABC=
| 1 |
| 2 |
点评:本题考查了熟练掌握导数的几何意义、直线的斜率与倾斜角的关系、直线与抛物线相交问题、弦长公式即可得出,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.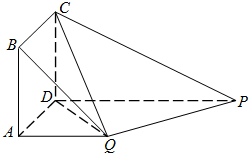 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=