Question

如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，侧面PAB⊥底面ABCD，PA=AD=AB=1，BC=2．
（1）求证：平面PBC⊥平面PDC；
（2）若∠PAB=90°，求二面角B-PD-C的正切值．

Answer 1

考点：异面直线及其所成的角,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）延长BA，CD交于M点，连接MP，则BM=2，A是BM的中点，AP=

1

2

BM，可得MP⊥PB．利用侧面PAB⊥底面ABCD，AB⊥BC，可得BC⊥MP，MP⊥平面PBC，即可证明；
（2）通过建立空间直角坐标系，求出两个平面的法向量，利用向量夹角公式即可得出．

解答： （1）证明：延长BA，CD交于M点，连接MP，则BM=2，
A是BM的中点，AP=

1

2

BM，
∴MP⊥PB，
又∵侧面PAB⊥底面ABCD，AB⊥BC，
∴BC⊥平面PBM，可得BC⊥MP，
故MP⊥平面PBC，
∵MP?平面PCD，∴平面PBC⊥平面PCD；
（2）解：∵∠PAB=90°，∴PA⊥平面ABCD，以AB，AD，AP分别为x，y，z轴，如图建立坐标系，
则B（1，0，0），D（0，1，0），P（0，0，1），M（-1，0，0），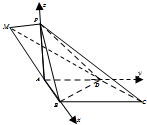

BD

=（-1，1，0），

BP

=（-1，0，1），

MP

=（1，0，1），

MD

=（1，1，0）．
设平面PBD的法向量为

m

=（x₁，y₁，z₁），可得

BP • m =0 BD • m =0

，
故

-x1+z1=0 -x1+y1=0

，可令x₁=1，得

m

=（1，1，1）．
设平面PMC的法向量为

n

=（x₂，y₂，z₂），可得

n • MP =0 n • MD =0

，
故

x1+z1=0 x1+y1=0

，可令x₁=1，得

n

=（1，-1，-1），
∴cos＜

m

，

n

＞=

m • n

| m || n |

=

-1

3 × 3

=-

1

3

．
设二面角B-PD-C为θ，则cosθ=

1

3

，tanθ=2

2

．

点评：本题考查了通过建立空间直角坐标系利用两个平面的法向量的夹角公式得出二面角、线面及面面垂直的判定与性质定理、直角三角形的判定定理等基础知识与基本技能方法，考查了空间想象能力，考查了推理能力，属于难题．