题目内容
12.已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)>f(x)g′(x),且f(x)=axg(x)(a>0,a≠1),$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,则实数a的值为2.分析 先根据题意设h(x)=$\frac{f(x)}{g(x)}$=ax,再求出其导数结合f′(x)g(x)>f(x)g′(x),判断出函数是增函数,然后根据$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$求出a的数值即可得到答案.
解答 解:根据题意可得:g(x)≠0,所以设h(x)=$\frac{f(x)}{g(x)}$=ax,
则h′(x)=$\frac{f′(x)g(x)-f(x)g′(x)}{{g}^{2}(x)}$=axlna
因为f′(x)g(x)>f(x)g′(x),
所以h′(x)>0,
所以函数h(x)是定义在R上的增函数.
又因为$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,
所以a+$\frac{1}{a}$=$\frac{5}{2}$
即2a2-5a+2=0,
所以a=2或a=$\frac{1}{2}$,
所以a=2.
故答案为2.
点评 本题考查导数的运算、导数与函数的单调性,考查学生灵活解决问题的能力,属于中档题

练习册系列答案
相关题目
2.已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x)>f′(x)对于x∈R恒成立(e为自然对数的底),则( )
| A. | e2015•f(2016)>e2016•f(2015) | |
| B. | e2016•f(2016)=e2016•f(2015) | |
| C. | e2015•f(2016)<e2016•f(2015) | |
| D. | e2015•f(2016)与e2016•f(2015)大小不确定 |
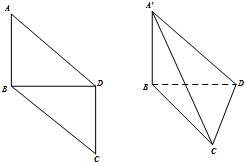 如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中:
如图,在平行四边形ABCD中,AB=BD=DC=1,AD=BC=$\sqrt{2}$,将平行四边形ABCD沿对角线BD折成三棱锥A′-BCD,使平面A′BD⊥平面BCD,在下列结论中: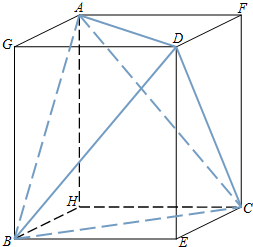 如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.
如图,长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD.