题目内容
9.已知抛物线y=ax2(a≠0)的准线方程为y=-1,焦点坐标为F(0,1).(1)求抛物线的方程;
(2)设F是抛物线的焦点,直线l;y=kx+b(k≠0)与抛物线相交于A,B两点,记AF,BF的斜率之和为m,求常数m,使得对于任意的实数k(k≠0),直线l恒过定点,并求出该定点的坐标.
分析 (1)将y=ax2,化为标准方程为x2=$\frac{y}{a}$,利用抛物线y=ax2(a≠0)的准线方程,即可求得抛物线C的方程;
(2)直线方程与抛物线方程联立$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}=4y}\end{array}\right.$,得x2-4kx-4b=0.利用韦达定理及直线AF,BF的斜率之和为m,可得直线l:y=kx+$\frac{k}{m-k}$,进而令xk2-(mx+y+1)k+my=0对任意的k(k≠0)恒成立,即可求得直线l过定点.
解答 解:(1)将y=ax2,化为标准方程为x2=$\frac{y}{a}$,
∴抛物线C的准线方程为:y=-$\frac{1}{4a}$.
∵抛物线y=ax2(a≠0)的准线方程为y=-1,
∴-$\frac{1}{4a}$=-1,解得a=$\frac{1}{4}$.
∴抛物线C的方程是x2=4y.
(2)F(0,1),设A(x1,$\frac{{{x}_{1}}^{2}}{4}$),B(x2,$\frac{{{x}_{2}}^{2}}{4}$),
由$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}=4y}\end{array}\right.$,得x2-4kx-4b=0.
∴x1+x2=4k,x1x2=-4b,△=16k2+16b>0.
kAF+kBF=$\frac{\frac{{{x}_{1}}^{2}}{4}-1}{{x}_{1}}$+$\frac{\frac{{{x}_{2}}^{2}}{4}-1}{{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})({x}_{1}{x}_{2}-4)}{4{x}_{1}{x}_{2}}$=$\frac{4k(-4b-4)}{4(-4b)}$. …
∴b=$\frac{k}{m-k}$.
∴直线l:y=kx+$\frac{k}{m-k}$.
令xk2-(mx+y+1)k+my=0对任意的k(k≠0)恒成立.
则$\left\{\begin{array}{l}{x=0}\\{mx+y+1=0}\\{my=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-1}\\{m=0}\end{array}\right.$.
所以m=0,直线l过定点(0,-1).
点评 本题考查抛物线的标准方程与性质,考查直线与抛物线的位置关系,考查直线恒过定点,解题的关键是求出直线方程,利用方程对任意的k(k≠0)恒成立,建立方程组.

 名校课堂系列答案
名校课堂系列答案| A. | {-1,0} | B. | {1} | C. | {-1,0,1} | D. | ∅ |
| A. | 2$\sqrt{1004}$ | B. | 1004 | C. | 2$\sqrt{2008}$ | D. | 2008 |
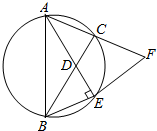 如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC到F,使得AC•AF=AD•AE,连按EF.
如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC到F,使得AC•AF=AD•AE,连按EF.