题目内容
如果函数f(x)是定义在R上的增函数,且f(x•y)=f(x)+f(y)对于任何实数x,y都成立,
(1)求f(0)的值;
(2)证明:f(
)=f(x)-f(y);
(3)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
(1)求f(0)的值;
(2)证明:f(
| x |
| y |
(3)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围.
考点:抽象函数及其应用
专题:计算题,证明题,函数的性质及应用
分析:(1)令x=y=0,则可求出f(0);
(2)令x=y=1,则f(1)=0,令xy=1,得到f(
)=-f(y),再由条件将y换成
,即可得证;
(3)由f(3)=1,得到f(9)=2.不等式等价为f(a)>f(9a-9),再由单调性即可解出a的范围.
(2)令x=y=1,则f(1)=0,令xy=1,得到f(
| 1 |
| y |
| 1 |
| y |
(3)由f(3)=1,得到f(9)=2.不等式等价为f(a)>f(9a-9),再由单调性即可解出a的范围.
解答:
(1)解:∵f(x•y)=f(x)+f(y),
∴令x=y=0,则f(0)=2f(0),
∴f(0)=0;
(2)证明:∵f(x•y)=f(x)+f(y),
∴令x=y=1,则f(1)=2f(1),
∴f(1)=0,
令xy=1,则x=
,f(1)=f(y)+f(
).
∴f(
)=-f(y),
∴f(
)=f(x)+f(
)=f(x)-f(y).
(3)解:∵f(3)=1,
∴f(9)=2f(3)=2.
则f(a)>f(a-1)+2,即为f(a)>f(a-1)+f(9),
即有f(a)>f(9a-9),
∵函数f(x)是定义在R上的增函数,
∴a>9a-9,
∴a<
.
则a的取值范围是(-∞,
).
∴令x=y=0,则f(0)=2f(0),
∴f(0)=0;
(2)证明:∵f(x•y)=f(x)+f(y),
∴令x=y=1,则f(1)=2f(1),
∴f(1)=0,
令xy=1,则x=
| 1 |
| y |
| 1 |
| y |
∴f(
| 1 |
| y |
∴f(
| x |
| y |
| 1 |
| y |
(3)解:∵f(3)=1,
∴f(9)=2f(3)=2.
则f(a)>f(a-1)+2,即为f(a)>f(a-1)+f(9),
即有f(a)>f(9a-9),
∵函数f(x)是定义在R上的增函数,
∴a>9a-9,
∴a<
| 9 |
| 8 |
则a的取值范围是(-∞,
| 9 |
| 8 |
点评:本题考查抽象函数及应用,考查解决抽象函数值的常用方法:赋值法,考查函数的单调性和运用,属于中档题.

练习册系列答案
相关题目
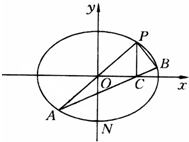 如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆
如图,在平面直角坐标系xOy中,过坐标原点的直线交椭圆