题目内容
函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
,
(1)确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性并用定义证明.
(3)解不等式f(2t-1)+f(t)<0.
| ax+b |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)确定函数f(x)的解析式;
(2)判断f(x)在(-1,1)上的单调性并用定义证明.
(3)解不等式f(2t-1)+f(t)<0.
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:(1)f(0)=0,且f(
)=
,求解.(2)运用定义判断证明,主要是作差分解因式判断
(3)利用奇偶性,单调性,转化2t-1<-t,解得;t<
,可得解集.
| 1 |
| 2 |
| 2 |
| 5 |
(3)利用奇偶性,单调性,转化2t-1<-t,解得;t<
| 1 |
| 3 |
解答:
解:(1)∵函数f(x)=
是定义在(-1,1)上的奇函数,
∴f(0)=0,即b=0
∵且f(
)=
,
∴a=1,
故函数f(x)的解析式f(x)=
,
(2)证明:f(x)=
,
设x1<x2,且在(-1,1)上,
f(x1)=
,f(x2)=
,
f(x1)-f(x2)=
∵x1<x2,且在(-1,1)上,
∴x1-x2<0,(1-x1x2)>0,(1+x
)>0,(1+x
)>0
即f(x1)<f(x2),
所以f(x)在(-1,1)上的单调递增.
(3)不等式f(2t-1)+f(t)<0,根据(1)(2)
即化为:不等式f(2t-1)<f(-t),
2t-1<-t,解得;t<
,
不等式f(2t-1)+f(t)<0的解集为:(-∞,
)
| ax+b |
| 1+x2 |
∴f(0)=0,即b=0
∵且f(
| 1 |
| 2 |
| 2 |
| 5 |
∴a=1,
故函数f(x)的解析式f(x)=
| x |
| 1+x2 |
(2)证明:f(x)=
| x |
| 1+x2 |
设x1<x2,且在(-1,1)上,
f(x1)=
| x1 | ||
1+
|
| x2 | ||
1+
|
f(x1)-f(x2)=
| (x1-x2)(1-x1x2) | ||||
(1+
|
∵x1<x2,且在(-1,1)上,
∴x1-x2<0,(1-x1x2)>0,(1+x
2 1 |
2 2 |
即f(x1)<f(x2),
所以f(x)在(-1,1)上的单调递增.
(3)不等式f(2t-1)+f(t)<0,根据(1)(2)
即化为:不等式f(2t-1)<f(-t),
2t-1<-t,解得;t<
| 1 |
| 3 |
不等式f(2t-1)+f(t)<0的解集为:(-∞,
| 1 |
| 3 |
点评:本题考查了函数的奇偶性,单调性,判断与运用,求解析式,解不等式,是基本题型,难度不大.

练习册系列答案
相关题目
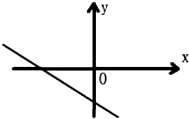
已知一次函数y=kx+b的图象如图所示,则k,b的符号是( )

| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b>0 |
| D、k<0,b<0 |
设U={1,2,3,4,5},若A∩B={2},(∁UA)∩B={4},(∁UA)∩(∁UB)={1,5},则下列结论正确的是( )
| A、3∉A且3∉B |
| B、3∈A且3∉B |
| C、3∉A且3∈B |
| D、3∈A且3∈B |
已知过点A(-2,m)和B(m,4)的直线l1与直线l2:2x+y-1=0垂直,则m的值为( )
| A、-8 | B、0 | C、2 | D、10 |