题目内容
某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费1.8元，超计划部分每吨按2.0元收费．
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：
①当用水量小于等于3000吨 ；②当用水量大于3000吨 ．
（2）某月该单位用水3200吨，水费是 元；若用水2800吨，水费 元．
（3）若某月该单位缴纳水费9400元，则该单位用水多少吨？
（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式：
①当用水量小于等于3000吨
（2）某月该单位用水3200吨，水费是
（3）若某月该单位缴纳水费9400元，则该单位用水多少吨？
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：（1）是个分段函数分①当用水量小于等于3000吨时和②当用水量大于3000吨时．
（2）根据给的用水量，然后代入函数值求解．
（3）代入f（x）=9400，从而可求出x的值．
（2）根据给的用水量，然后代入函数值求解．
（3）代入f（x）=9400，从而可求出x的值．
解答：
解：（1）单位水费f（x）（元）和每月用水量x（吨），
当x≤3000吨时；f（x）=1.8x，
当x＞3000吨时：f（x）=3000×1.8+2.0（x-3000）=2x-600，
∴f（x）=
；
（2）单位用水3200吨，水费是：f（3200）=2×3200-600=5800（元），
若用水2800吨，水费：f（2800）=1.8×2800=5040（元）；
故答案为：f（x）=
；f（x）=1.8x，f（x）=2x-600，
5800，5040，
（3）当该单位缴纳水费9400元，则9400=2x-600，解得x=5000，
故该单位用水5000吨．
当x≤3000吨时；f（x）=1.8x，
当x＞3000吨时：f（x）=3000×1.8+2.0（x-3000）=2x-600，
∴f（x）=
|
（2）单位用水3200吨，水费是：f（3200）=2×3200-600=5800（元），
若用水2800吨，水费：f（2800）=1.8×2800=5040（元）；
故答案为：f（x）=
|
5800，5040，
（3）当该单位缴纳水费9400元，则9400=2x-600，解得x=5000，
故该单位用水5000吨．
点评：本题考查一次函数的应用，关键是知道是分段函数，且用水量和钱数之间的关系，从而求解．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
下面哪个点不在函数y=-2x+3的图象上（ ）
| A、（-5，13） |
| B、（0.5，2） |
| C、（3，0） |
| D、（1，1） |
函数y=（m+1）x-（4m-3）的图象在第一、二、四象限，那么m的取值范围是（ ）
A、m＜
| ||
B、-1＜m＜
| ||
| C、m＜-1 | ||
| D、m＞-1 |
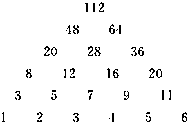给定正整数n（n≥2）按下图方式构成三角形数表；第一行依次写上数1，2，3，…，n，在下面一行的每相邻两个数的正中间上方写上这两个数之和，得到上面一行的数（比下一行少一个数），依此类推，最后一行（第n行）只有一个数．例如n=6时数表如图所示，则当n=2007时最后一行的数是 （ ）| A、251×22007 |
| B、2007×22006 |
| C、251×22008 |
| D、2007×22005 |