题目内容
13.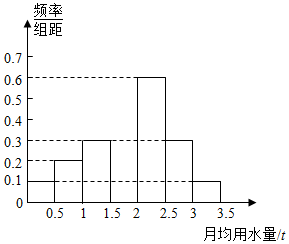 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准〜则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的众数,中位数,平均数(同一组中的数据用该区间的中点值代表).
分析 (1)根据题意确定出1.5-2t用户的$\frac{频率}{组距}$,补全频率分布直方图即可;
(2)月均用水量的最低标准应定为2.5吨,理由为:样本中月均用水量不低于2.5吨的居民有20位,占样本总体的20%,根据样本估计总体作出解释即可;
(3)找出居民用水量的众数,中位数,求出平均数即可.
解答 解:(1)根据题意得:1.5-2t的用户的$\frac{频率}{组距}$=0.4,如图所示: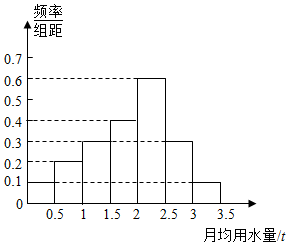
(2)月均用水量的最低标准应定为2.5吨,理由为:
样本中月均用水量不低于2.5吨的居民有20位,占样本总体的20%,
由样本估计总体,要保证80%的居民每月的用水量不超出标准,月均用水量的最低标准应定为2.5吨;
(3)这100位居民的月均用水量的众数2.25,中位数2,
平均数为0.5×($\frac{1}{4}$×0.10+$\frac{3}{4}$×0.20+$\frac{5}{4}$×0.30+$\frac{7}{4}$×0.40+$\frac{9}{4}$×0.60+$\frac{11}{4}$×0.30+$\frac{13}{4}$×0.10)=1.875.
点评 此题考查了众数,中位数,平均数,以及频数分布直方图,弄清题中的数据是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
4.已知命题p:?x0∈(0,2],使$x_0^2-a{x_0}+1<0$,若?p是真命题,则实数a的取值范围为( )
| A. | (-∞,2) | B. | (-∞,2] | C. | [-2,2] | D. | (-∞,-2)∪(2,+∞) |
18.已知圆C的标准方程是(x-2)2+(y-4)2=k(k>0),若圆C与y轴交于A,B两点,且点A在点B的上方,圆C与x轴交于E,F两点,且点E在点F的右方,则AE中点M的轨迹方程是( )
| A. | (y-2)2-(x-1)2=3(x>1,y>2+$\sqrt{3}$) | B. | (y-2)2-(x-1)2=3 | ||
| C. | (x-2)2-(y-1)2=3(y>1,x>2+$\sqrt{3}$) | D. | (x-2)2-(y-1)2=3 |
5.函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}-10}$与数列{an}的通项公式an=$\frac{{2}^{n}-1}{{2}^{n}-10}$,则下列说法正确的是( )
| A. | 函数f(x)有最大值,数列{an}有最大项 | B. | 函数f(x)有最大值,数列{an}无最大项 | ||
| C. | 函数f(x)无最大值,数列{an}有最大项 | D. | 函数f(x)无最大值,数列{an}无最大项 |
3.已知点C在线段AB上,且$\overrightarrow{AC}$=$\frac{2}{7}$$\overrightarrow{CB}$,则( )
| A. | $\overrightarrow{AB}$=$\frac{7}{5}\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$=-$\frac{7}{5}\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$=$\frac{9}{7}\overrightarrow{BC}$ | D. | $\overrightarrow{AB}$=-$\frac{9}{7}\overrightarrow{BC}$ |