题目内容
1.(1)若直线l1与l2互相垂直,且方程分别为l1:2x+y+2=0,l2:ax+4y-2=0,求它们交点坐标;(2)求经过点(-2,-3),在x轴、y轴上截距相等的直线方程.
分析 (1)根据两直线垂直,斜率之积等于-1,求出a=-2,把两直线的方程联立方程组求得交点的坐标;
(2)分类讨论,当直线过原点,即截距都为零,易得直线方程;当直线不过原点,由截距式,设出直线方程,把P点坐标带入,能求出结果.
解答 解:(1)由题意可得-2×(-$\frac{a}{4}$)=-1,∴a=-2.
两直线即2x+y+2=0与-2x+4y-2=0.
联立两直线方程,
可得交点的坐标为(-1,0),
(2)当直线过原点,即截距都为零时,
直线经过原点(0,0),P(-2,-3),
直线方程为$\frac{y}{x}$=$\frac{-3}{-2}$,
整理,得直线方程为3x-2y=0;
当直线不过原点,
由截距式,设直线方程为 $\frac{x}{a}$+$\frac{y}{a}$=1,
把P(-2,-3)代入,得x+y+5=0.
故直线方程是:x+y+5=0或3x-2y=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
9.下列命题中,正确的是( )
| A. | 若z是复数,则|z|2=z2 | |
| B. | 任意两个复数不能比较大小 | |
| C. | 当b2-4ac>0时,一元二次方程ax2+bx+c=0(a、b、c∈C)有两个不相等的实数根 | |
| D. | 在复平面xOy上,复数z=m2+mi(m∈R,i是虚数单位)对应的点的轨迹方程是y2=x |
16.直线$3x+\sqrt{3}y+2=0$的倾角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
6.命题“任意x∈R,|x|≥0”的否定是( )
| A. | 任意x∈R,|x|<0 | B. | 任意x∈R,|x|≤0 | C. | 彐x∈R,|x|<0 | D. | 彐x∈R,|x|≤0 |
11.直线x+2y=2,则x2+y2的最小值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
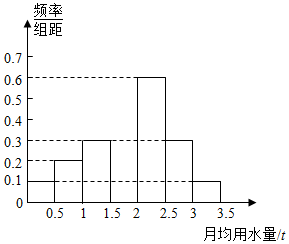 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.