题目内容
2.已知数列{an}中,a1=m,an+1=$\left\{\begin{array}{l}{16{n}^{2}{,a}_{n}<16{n}^{2}}\\{2{a}_{n},{a}_{n}≥16{n}^{2}}\end{array}\right.$ (n∈N*),若{an}为等比数列,则实数m的取值范围是{m|m≥16或m=8}.分析 由已知得当m<16时,由等比数列的性质推导出a1=m=8;当m≥16时,${a}_{n}=m×{2}^{n-1}$.由此能求出实数m的取值范围.
解答 解:∵a1=m,an+1=$\left\{\begin{array}{l}{16{n}^{2}{,a}_{n}<16{n}^{2}}\\{2{a}_{n},{a}_{n}≥16{n}^{2}}\end{array}\right.$ (n∈N*),{an}为等比数列
∴当m<16时,a2=16,a3=32,a4=64,an=8×2n-1,∴a1=m=8;
当m≥16时,a2=2m,a3=4m,a4=8m,${a}_{n}=m×{2}^{n-1}$.
综上,实数m的取值范围是{m|m≥16或m=8}.
故答案为:{m|m≥16或m=8}.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知$\overrightarrow{AB}$=-$\frac{3}{2}$$\overrightarrow{BC}$,$\overrightarrow{BD}$=-$\frac{3}{5}$$\overrightarrow{DC}$,若$\overrightarrow{AC}$=$λ\overrightarrow{CD}$,则λ等于( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
11.直线x+2y=2,则x2+y2的最小值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
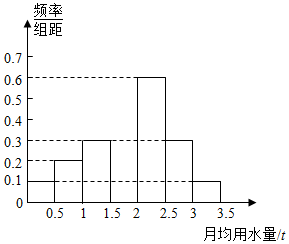 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.