题目内容
3.已知函数f(x)=2cos[ω(x+φ)](ω>0,0<φ<π).(1)若函数f(x)图象过点(0,-2)且图象上两个对称中心A(x1,0)与B(x2,0)间最短距离为$\frac{π}{2}$,求函数f(x)解析式;
(2)若$φ=\frac{π}{2}$,函数f(x)在[-$\frac{π}{3},\frac{2π}{3}$]上单调递减,求ω的取值范围.
分析 (1)由题意可得函数f(x)的周期,可得ω值,代点可得φ值,可得解析式;
(2)由x的范围结合余弦函数的单调性可得ω的范围.
解答 解:(1)∵f(x)图象上两个对称中心A(x1,0)与B(x2,0)间最短距离为$\frac{π}{2}$,
∴函数f(x)的周期T=π,∴ω=$\frac{2π}{T}$=2,
又f(0)=2cos2φ=-2,即cos2φ=-1,
∵0<φ<π,∴0<2φ<2π,∴2φ=π,∴φ=$\frac{π}{2}$,
∴f(x)=2cos[2(x+$\frac{π}{2}$)]=-2sin2x;
(2)∵x∈[-$\frac{π}{3},\frac{2π}{3}$],∴x+$\frac{π}{2}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∵ω>0,函数f(x)在[-$\frac{π}{3},\frac{2π}{3}$]上单调递减,
∴根据题意有$\frac{ωπ}{6}$≥2kπ且$\frac{7ωπ}{6}$≤2kπ+π,
解得12k≤ω≤$\frac{12k+6}{7}$,k∈Z
结合题意可得k=0时,0<ω≤$\frac{6}{7}$.
点评 本题考查余弦函数图象,涉及函数的单调性,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
7.A={x|x>0},B={x|x2-1<0},A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x>1} | C. | {x|x>0} | D. | {x|0<x<1} |
15.已知a=31.2,b=3°,$c={({\frac{1}{3}})^{-0.9}}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
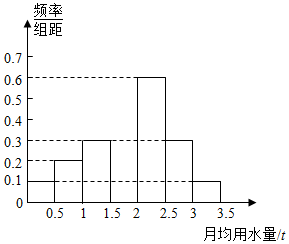 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.