题目内容
4.已知命题p:?x0∈(0,2],使$x_0^2-a{x_0}+1<0$,若?p是真命题,则实数a的取值范围为( )| A. | (-∞,2) | B. | (-∞,2] | C. | [-2,2] | D. | (-∞,-2)∪(2,+∞) |
分析 根据特称命题的否定是全称命题结合命题的真假关系进行判断求解即可.
解答 解:∵命题p:?x0∈(0,2],使$x_0^2-a{x_0}+1<0$的否定¬p:?x∈(0,2],x2-ax+1≥0,
即x2+1≥ax,即a≤x+$\frac{1}{x}$,
设f(x)=x+$\frac{1}{x}$,则f(x)=x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当且仅当x=$\frac{1}{x}$,即x=1时,取等号,
∴a≤2,
故选:B.
点评 本题主要考查含有量词的命题的否定的应用,根据条件利用参数分离法进行转化,结合基本不等式求最值是解决本题的关键.

练习册系列答案
相关题目
15.已知a=31.2,b=3°,$c={({\frac{1}{3}})^{-0.9}}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
9.下列命题中,正确的是( )
| A. | 若z是复数,则|z|2=z2 | |
| B. | 任意两个复数不能比较大小 | |
| C. | 当b2-4ac>0时,一元二次方程ax2+bx+c=0(a、b、c∈C)有两个不相等的实数根 | |
| D. | 在复平面xOy上,复数z=m2+mi(m∈R,i是虚数单位)对应的点的轨迹方程是y2=x |
16.直线$3x+\sqrt{3}y+2=0$的倾角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
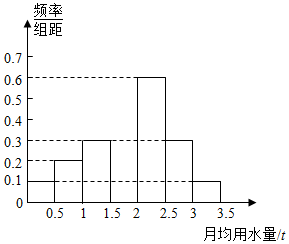 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.