函数f(x)=2x-x2的零点的个数为( )A．1 个B．2 个C．3 个D．4 个题目和参考答案——青夏教育精英家教网—

题目内容

8．函数f（x）=2^x-x²的零点的个数为（　　）

A．

1 个

B．

2 个

C．

3 个

D．

4 个

分析这道题可先在同一个坐标系中画出函数y=2^x与y=x²的图象，然后问题可转化为该两个函数图象交点的个数问题，结合计算可解决问题．

解答解：f（x）=2^x-x²的零点，即为2^x-x²=0的根，也就是函数y=2^x与y=x²的图象交点的横坐标，
作出这两个函数的图象如下：

由图可知，当x＜0时，必有一个交点，当x≥0时，结合图象，且x=2及x=4都是该方程的解，故原函数共有3个不同的零点．
故答案：C

点评本题考查了函数零点的概念及性质．此例的关键在于能够将问题转化为两个函数图象交点的个数问题，然后画出图象结合计算解决问题．

练习册系列答案

若a＜b＜0，则$\frac{1}{a}＞\frac{1}{b}$

B．

若$\frac{1}{a}＞1$，则0＜a＜1

C．

若a＞b＞0，则a⁴＞b⁴

D．

若a＜1，则$\frac{1}{a}＜1$

16．直三棱柱ABC-A₁B₁C₁的六个顶点都在直径为$\sqrt{269}$的球面上，且AB=5，AC=12，BC=13，点D是BB₁的中点，则AD与平面BCC₁B₁所成角的正弦值为（　　）

$\frac{6\sqrt{2}}{13}$

D．

$\frac{5\sqrt{2}}{13}$

3．已知f（x）=x⁵+ax³+bx-10，且f（-3）=10，则f（3）=-30．

13．已知函数f（x）=a^x-（k-1）a^-x（a＞1）是定义在R 上的奇函数．
（1）求k 的值并判断函数 f （x）单调性；
（2）若f（1）=$\frac{3}{2}$，且g（x）=a^2x+a^-2x-2mf（x）在[1，+∞）上的最小值为-2，求m的值．

20．

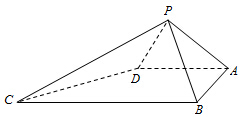四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠BCD=45°．△PAB与△PAD都是等边三角形．
（1）求证：CD⊥平面PBD；
（2）求直线CD与平面PAD所成角的正弦值．

17．从1，2，3，4，5这5个数字中任选2个数字，则这2个数字之和为偶数的概率为（　　）

18．已知$\overrightarrow{a}$=（cos$\frac{3x}{2}$，sin$\frac{3x}{2}$），$\overrightarrow{b}$=（cos$\frac{x}{2}$，sin$\frac{x}{2}$），定义函数f（x）=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}+\overrightarrow{b}|}$．
（1）求|2$\overrightarrow{a}$-3$\overrightarrow{b}$|的最大值；
（2）当0≤x≤$\frac{2π}{3}$时，求函数f（x）的值域．

试题分类