题目内容
已知幂函数y=x（m-6）（m∈Z）与y=x（2-m）（m∈Z）的图象与x轴、y轴都无公共点，且y=x（m-2）（m∈Z）的图象关于y轴对称，求m的值．
考点：幂函数的概念、解析式、定义域、值域
专题：函数的性质及应用
分析：由已知条件推导出m-6＜0，且2-m＜0，m-2为偶数，由此能求出m的值．
解答：
解：∵幂函数y=x（m-6）（m∈Z）与y=x（2-m）（m∈Z）的图象与x、y轴没有公共点，
∴m-6＜0，且2-m＜0，
解得2＜m＜6，
∴m的可能取值为3，4，5，
又∵y=x（m-2）的图象关于y轴对称，
∴y=x（m-2）为偶函数，即m-2为偶数，
∴m=4．
∴m-6＜0，且2-m＜0，
解得2＜m＜6，
∴m的可能取值为3，4，5，
又∵y=x（m-2）的图象关于y轴对称，
∴y=x（m-2）为偶函数，即m-2为偶数，
∴m=4．
点评：本题考查满足条件的实数值的求法，是基础题，解题时要认真审题，注意幂函数性质的灵活运用．
练习册系列答案
相关题目
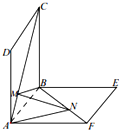如图正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直．点M在AC上移动，点N在BF上移动，若CM=BN=a（0＜a＜