题目内容
设函数f(x)=exu(x),
(Ⅰ)若u(x)=x2-
x+2,求函数f(x)的单调递增区间;
(Ⅱ)若u(x)=x2+ax-3-2a,设函数g(x)=(a2+14)ex+4.当a>0时,分别求出f(x)和g(x)在x∈[0,4]的值域.
(Ⅰ)若u(x)=x2-
| 5 |
| 2 |
(Ⅱ)若u(x)=x2+ax-3-2a,设函数g(x)=(a2+14)ex+4.当a>0时,分别求出f(x)和g(x)在x∈[0,4]的值域.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(Ⅰ)化简函数并求导,令导数大于0,从而解出增区间;(Ⅱ)求导确定函数的单调区间,由单调区间求函数的最值,进而求值域.
解答:
解:(Ⅰ)f(x)=exu(x)=(x2-
x+2)ex,
f′(x)=(x2-
x-
)ex,
令f′(x)>0,得x<-
或x>1,
则函数f(x)的单调递增区间为(-∞,-
),(1,+∞).
(Ⅱ)f(x)=(x2+ax-3-2a)ex,
当a>0时,f(x)在(0,1)上单调递减,在区间(1,4)上单调递增;
∴f(x)≥f(1)=-(a+2)e;
又∵f(0)=-(2a+3)<0,f(4)=(2a+13)e4>0
∴函数f(x)在区间[0,4]上的值域是[-(a+2)e,(2a+13)e4].
又g(x)=(a2+14)ex+4在区间[0,4]上是增函数,所以它在区间[0,4]上的值域是[(a2+14)e4,(a2+14)e8].
| 5 |
| 2 |
f′(x)=(x2-
| 1 |
| 2 |
| 1 |
| 2 |
令f′(x)>0,得x<-
| 1 |
| 2 |
则函数f(x)的单调递增区间为(-∞,-
| 1 |
| 2 |
(Ⅱ)f(x)=(x2+ax-3-2a)ex,
当a>0时,f(x)在(0,1)上单调递减,在区间(1,4)上单调递增;
∴f(x)≥f(1)=-(a+2)e;
又∵f(0)=-(2a+3)<0,f(4)=(2a+13)e4>0
∴函数f(x)在区间[0,4]上的值域是[-(a+2)e,(2a+13)e4].
又g(x)=(a2+14)ex+4在区间[0,4]上是增函数,所以它在区间[0,4]上的值域是[(a2+14)e4,(a2+14)e8].
点评:本题考查了导数的综合应用,及函数值域的求法,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
(文)若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,有下面四个结论:
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等
③连接四面体ABCD每组对棱中点的线段互垂直平分;
④从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边
其中正确结论的个数有( )
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等
③连接四面体ABCD每组对棱中点的线段互垂直平分;
④从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边
其中正确结论的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,若(a2+c2-b2)sinB=
ac,则角B的值为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
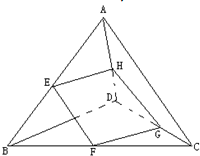 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.