题目内容
7.已知向量$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(sinβ,cosβ).(1)求|$\overrightarrow{a}$$+\overrightarrow{b}$|的最小值;
(2)若向量$\overrightarrow{c}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),且$\overrightarrow{b}$$•\overrightarrow{c}$=$\frac{3}{5}$,β∈(0,π),求sinβ的值.
分析 (1)由已知求得$\overrightarrow{a}$$+\overrightarrow{b}$的坐标,代入模的公式化简,则|$\overrightarrow{a}$$+\overrightarrow{b}$|的最小值可求;
(2)利用数量积求得$sin(β-\frac{π}{3})=-\frac{3}{5}$,结合角的范围及平方关系求得cos($β-\frac{π}{3}$),再利用“拆角、配角”方法求得sinβ的值.
解答 解:(1)∵$\overrightarrow{a}$=(2cosα,2sinα),$\overrightarrow{b}$=(sinβ,cosβ),
∴$\overrightarrow{a}+\overrightarrow{b}=(2cosα+sinβ,2sinα+cosβ)$,
则$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(2cosα+sinβ)^{2}+(2sinα+cosβ)^{2}}$
=$\sqrt{4co{s}^{2}α+4cosαsinβ+si{n}^{2}β+4si{n}^{2}α+4sinαcosβ+co{s}^{2}β}$
=$\sqrt{5+4sin(α+β)}$.
∴当sin(α+β)=-1时,$|\overrightarrow{a}+\overrightarrow{b}{|}_{min}=1$;
(2)由$\overrightarrow{b}$=(sinβ,cosβ),$\overrightarrow{c}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),且$\overrightarrow{b}$$•\overrightarrow{c}$=$\frac{3}{5}$,
得$-\frac{1}{2}sinβ+\frac{\sqrt{3}}{2}cosβ$=$-sin(β-\frac{π}{3})=\frac{3}{5}$,
即$sin(β-\frac{π}{3})=-\frac{3}{5}$,
∵β∈(0,π),∴$-\frac{π}{3}<β-\frac{π}{3}<\frac{2π}{3}$,
∴cos($β-\frac{π}{3}$)=$\sqrt{1-(-\frac{3}{5})^{2}}=\frac{4}{5}$,
则sinβ=sin[($β-\frac{π}{3}$)+$\frac{π}{3}$]=sin($β-\frac{π}{3}$)cos$\frac{π}{3}$+cos($β-\frac{π}{3}$)sin$\frac{π}{3}$
=$-\frac{3}{5}×\frac{1}{2}+\frac{4}{5}×\frac{\sqrt{3}}{2}=\frac{4\sqrt{3}-3}{10}$.
点评 本题考查平面向量的数量积运算,考查了三角函数中的恒等变换运用,考查计算能力,是中档题.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案| A. | [$\frac{1}{7}$,+∞) | B. | [$\frac{1}{7}$,$\frac{1}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{7}$]∪($\frac{1}{3}$,+∞) |
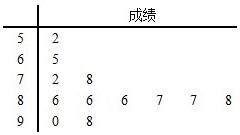 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.