题目内容
17．已知a＞b，a-$\frac{1}{a}$＞b-$\frac{1}{b}$同时成立，则a，b应满足的条件是ab＞0或ab＜-1．．分析 由a＞b，a-$\frac{1}{a}$＞b-$\frac{1}{b}$同时成立得到$\frac{1}{ab}$＞-1，通过讨论ab的符号，求出答案即可．
解答 解：∵a-$\frac{1}{a}$＞b-$\frac{1}{b}$，
a-b＞$\frac{1}{a}$-$\frac{1}{b}$=-$\frac{a-b}{ab}$ ①
∵a-b＞0，
所以由 ①两边同除a-b得
∴$\frac{1}{ab}$＞-1 ②
下面分别讨论
（1）当ab＞0（同号）时，②式恒成立
（2）当ab＜0（异号）时，要使②式成立，必须使ab＜-1
综合（1）（2）
可知ab应满足的条件是ab＞0 或ab＜-1，
故答案为：ab＞0或ab＜-1．
点评 本题考查了不等式的基本性质，考查转化思想，分类讨论思想，是一道基础题．
练习册系列答案
相关题目
7．设关于x、y的不等式组$\left\{\begin{array}{l}{2x-y+1＞0}\\{3x-2＜0}\\{y-a＞0}\end{array}\right.$表示的平面区域内存在点P（x0，y0），满足x0-2y0=2，则a的取值范围是（ ）
| A． | （-∞，-$\frac{5}{3}$） | B． | （-∞，-$\frac{2}{3}$） | C． | （-∞，$\frac{1}{3}$） | D． | （-∞，$\frac{4}{3}$） |
5．已知函数$y=2sin（2x+φ）（|φ|＜\frac{π}{2}）$的图象经过点（0，-1），则该函数的一个单调递增区间为（ ）
| A． | [-$\frac{π}{6}$，$\frac{π}{3}$] | B． | [$\frac{π}{3}$，$\frac{5π}{6}$] | C． | [-$\frac{5π}{12}$，$\frac{π}{12}$] | D． | [$\frac{π}{12}$，$\frac{7π}{12}$]] |
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为f（x）=2sin（$\frac{π}{3}$x+$\frac{π}{6}$）．
2．
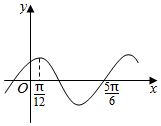设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）
设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）| A． | f（-$\frac{3π}{4}$）＜f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$） | B． | f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$）＜f（$\frac{5π}{3}$） | C． | f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$）＜f（-$\frac{3π}{4}$） | D． | f（$\frac{5π}{3}$）＜f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$） |