题目内容
12．已知数列{an}为等差数列．（1）若a1-a4-a8-a12+a15=2，求a3+a13的值；
（2）若a9+a10=a，a19+a20=b，求a99+a100．
分析 （1）由已知结合等差数列的性质求得a8，则a3+a13等于2a8可求；
（2）利用等差数列的性质，a9+a10，a19+a20…a99+a100仍成等差数列，利用等差数列的通项公式可求得答案．
解答 解：在等差数列{an}中，
（1）由a1-a4-a8-a12+a15=2，得
（a1+a15）-（a4+a8+a12）=2，
即2a8-3a8=2，∴a8=-2，
∴a3+a13=2a8=-4；
（2）∵{an}为等差数列，
∴a9+a10，a19+a20…a99+a100仍成等差数列，且公差为b-a，
由已知得a99+a100=a+9•（b-a）=9b-8a．
点评 本题考查等差数列的性质与通项公式，关键在于对性质的灵活运用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
2．
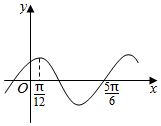设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）
设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（ ）| A． | f（-$\frac{3π}{4}$）＜f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$） | B． | f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$）＜f（$\frac{5π}{3}$） | C． | f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$）＜f（-$\frac{3π}{4}$） | D． | f（$\frac{5π}{3}$）＜f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$） |
17．已知函数f（x）=cos（4x-$\frac{π}{3}$）+2cos2（2x），将函数y=f（x）的图象上所有点的横坐标伸长为原来的2倍，纵坐标不变，再将所得函数图象向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，则函数y=g（x）的一个单调递增区间为（ ）
| A． | [-$\frac{π}{3}$，$\frac{π}{6}$] | B． | [-$\frac{π}{4}$，$\frac{π}{4}$] | C． | [$\frac{π}{6}$，$\frac{2π}{3}$] | D． | [$\frac{π}{4}$，$\frac{3π}{4}$] |
如图，ABCD是平行四边形，EA⊥平面ABCD，PD∥EA，BD=PD=2EA=4，AD=3，AB=5．F，G，H分别为PB，EB，PC的中点．
3．设f（x）=$\left\{\begin{array}{l}{4{x}^{3}+6{x}^{2}+2（x≤0）}\\{2{e}^{ax}（x＞0）}\end{array}\right.$在区间[-2，2]上最大值为4，则实数a的取值范围为（ ）
| A． | [$\frac{1}{2}$ln2，+∞] | B． | [0，$\frac{1}{2}$ln2] | C． | （-∞，0] | D． | （-∞，$\frac{1}{2}$ln2] |