题目内容
18.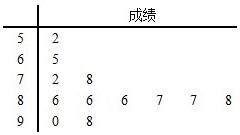 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.(Ⅰ)将频率视为概率.根据样本估计总体的思想,在该社区全体老年人中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(Ⅱ)从抽取的12人中随机选取3人,记ξ表示成绩“优良”的人数,求ξ的分布列及期望.
分析 (Ⅰ)从该社区中任选1人,成绩是“优良”的概率为$\frac{2}{3}$,由此利用对立事件概率计算公式能求出至少有1人成绩是“优良”的概率.
(Ⅱ)由题意可得,ξ的可能取值为0,1,2,3.分别求出相应的概率,由此能求出ξ的分布列及期望.
解答 解:(Ⅰ)抽取的12人中成绩是“优良”的频率为$\frac{2}{3}$,
故从该社区中任选1人,成绩是“优良”的概率为$\frac{2}{3}$,…(2分)
设“在该社区老人中任选3人,至少有1人成绩是‘优良’的事件”为A,
则$P(A)=1-C_3^0×{(1-\frac{2}{3})^3}=1-\frac{1}{27}=\frac{26}{27}$; …(5分)
(Ⅱ)由题意可得,ξ的可能取值为0,1,2,3.
$P(ξ=0)=\frac{C_4^3}{{C_{12}^3}}=\frac{4}{220}=\frac{1}{55}$,
$P(ξ=1)=\frac{C_8^1C_4^2}{{C_{12}^3}}=\frac{48}{220}=\frac{12}{55}$,
$P(ξ=2)=\frac{C_8^2C_4^1}{{C_{12}^3}}=\frac{112}{220}=\frac{28}{55}$,
$P(ξ=3)=\frac{C_8^3}{{C_{12}^3}}=\frac{56}{220}=\frac{14}{55}$,…(9分)
所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{55}$ | $\frac{12}{55}$ | $\frac{28}{55}$ | $\frac{14}{55}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.设f(x)=$\left\{\begin{array}{l}{4{x}^{3}+6{x}^{2}+2(x≤0)}\\{2{e}^{ax}(x>0)}\end{array}\right.$在区间[-2,2]上最大值为4,则实数a的取值范围为( )
| A. | [$\frac{1}{2}$ln2,+∞] | B. | [0,$\frac{1}{2}$ln2] | C. | (-∞,0] | D. | (-∞,$\frac{1}{2}$ln2] |
 如图,ABCD是平行四边形,EA⊥平面ABCD,PD∥EA,BD=PD=2EA=4,AD=3,AB=5.F,G,H分别为PB,EB,PC的中点.
如图,ABCD是平行四边形,EA⊥平面ABCD,PD∥EA,BD=PD=2EA=4,AD=3,AB=5.F,G,H分别为PB,EB,PC的中点.