题目内容
已知△ABC的内角A,B,C满足sin2A+sin(A-B+C)=sin(C-A-B)+
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
| 1 |
| 2 |
| A、bc(b+c)>8 | ||
B、ab(a+b)>16
| ||
| C、6≤abc≤12 | ||
| D、12≤abc≤24 |
考点:正弦定理的应用,二倍角的正弦
专题:三角函数的求值,解三角形
分析:根据正弦定理和三角形的面积公式,利用不等式的性质 进行证明即可得到结论.
解答:
解:∵△ABC的内角A,B,C满足sin2A+sin(A-B+C)=sin(C-A-B)+
,
∴sin2A+sin2B=-sin2C+
,
∴sin2A+sin2B+sin2C=
,
∴2sinAcosA+2sin(B+C)cos(B-C)=
,
2sinA(cos(B-C)-cos(B+C))=
,
化为2sinA[-2sinBsin(-C)]=
,
∴sinAsinBsinC=
.
设外接圆的半径为R,
由正弦定理可得:
=
=
=2R,
由S=
absinC,及正弦定理得sinAsinBsinC=
=
,
即R2=4S,
∵面积S满足1≤S≤2,
∴4≤R2≤8,即2≤R≤2
,
由sinAsinBsinC=
可得8≤abc≤16
,显然选项C,D不一定正确,
A.bc(b+c)>abc≥8,即bc(b+c)>8,正确,
B.ab(a+b)>abc≥8,即ab(a+b)>8,但ab(a+b)>16
,不一定正确,
故选:A
| 1 |
| 2 |
∴sin2A+sin2B=-sin2C+
| 1 |
| 2 |
∴sin2A+sin2B+sin2C=
| 1 |
| 2 |
∴2sinAcosA+2sin(B+C)cos(B-C)=
| 1 |
| 2 |
2sinA(cos(B-C)-cos(B+C))=
| 1 |
| 2 |
化为2sinA[-2sinBsin(-C)]=
| 1 |
| 2 |
∴sinAsinBsinC=
| 1 |
| 8 |
设外接圆的半径为R,
由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
由S=
| 1 |
| 2 |
| S |
| 2R2 |
| 1 |
| 8 |
即R2=4S,
∵面积S满足1≤S≤2,
∴4≤R2≤8,即2≤R≤2
| 2 |
由sinAsinBsinC=
| 1 |
| 8 |
| 2 |
A.bc(b+c)>abc≥8,即bc(b+c)>8,正确,
B.ab(a+b)>abc≥8,即ab(a+b)>8,但ab(a+b)>16
| 2 |
故选:A
点评:本题考查了两角和差化积公式、正弦定理、三角形的面积计算公式、基本不等式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
“a>m>1”是“logam<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为5,则|AB|等于( )
| A、12 | B、8 | C、6 | D、4 |
已知两点A(-1,5),B(3,9),则线段AB的中点坐标为( )
| A、(1,7) |
| B、(2,2) |
| C、(-2,-2) |
| D、(2,14) |
为得到函数y=cos2x的图象,只需将函数y=
的图象按照向量
平移,则
可以为( )
| sin2x |
| 2 |
| a |
| a |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
对任意的实数k,直线y=kx+1与圆x2+y2=2的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、随k的变化而变化 |
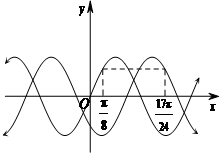 已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )
已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )A、
| ||
B、
| ||
C、
| ||
D、
|