题目内容
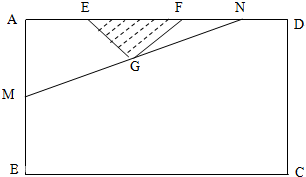 某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)
某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m)(1)将五边形MBCDN的面积y表示为x的函数;
(2)当x为何值时,市民健身广场的面积最大?并求出最大面积.
考点:基本不等式在最值问题中的应用
专题:应用题,不等式的解法及应用
分析:(1)作GH⊥EF,垂足为H,过M作MT∥BC交CD于T,求出AM=
,可得SMBCDW=SMBCT+SMTDN=(40-AM)×60+
(x+60)×AM,从而可得五边形MBCDN的面积y表示为x的函数;
(2)将函数变形,利用基本不等式,可求市民健身广场的面积最大值.
| 600-10x |
| 40-x |
| 1 |
| 2 |
(2)将函数变形,利用基本不等式,可求市民健身广场的面积最大值.
解答:
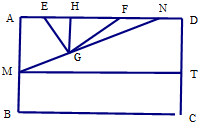 解:(1)作GH⊥EF,垂足为H,
解:(1)作GH⊥EF,垂足为H,
因为DN=x,所以NH=40-x,NA=60-x,
因为
=
,
所以
=
,所以AM=
…(2分)
过M作MT∥BC交CD于T,
则SMBCDW=SMBCT+SMTDN=(40-AM)×60+
(x+60)×AM,
所以y=(40-
)×60+
×
=2400-
…(7分)
由于N与F重合时,AM=AF=30适合条件,故x∈(0,30],…(8分)
(2)y=2400-
=2400-5[(40-x)+
+40],…(10分)
所以当且仅当40-x=
,即x=20∈(0,30]时,y取得最大值2000,…(13分)
所以当DN=20m时,得到的市民健身广场面积最大,最大面积为2000m2.…(14分)
 解:(1)作GH⊥EF,垂足为H,
解:(1)作GH⊥EF,垂足为H,因为DN=x,所以NH=40-x,NA=60-x,
因为
| NH |
| HG |
| NA |
| AM |
所以
| 40-x |
| 10 |
| 60-x |
| AM |
| 600-10x |
| 40-x |
过M作MT∥BC交CD于T,
则SMBCDW=SMBCT+SMTDN=(40-AM)×60+
| 1 |
| 2 |
所以y=(40-
| 600-10x |
| 40-x |
| 1 |
| 2 |
| (x+60)(600-10x) |
| 40-x |
| 5(60-x)2 |
| 40-x |
由于N与F重合时,AM=AF=30适合条件,故x∈(0,30],…(8分)
(2)y=2400-
| 5(60-x)2 |
| 40-x |
| 400 |
| 40-x |
所以当且仅当40-x=
| 400 |
| 40-x |
所以当DN=20m时,得到的市民健身广场面积最大,最大面积为2000m2.…(14分)
点评:基本不等式应注意其使用条件:一正二定三相等.

练习册系列答案
相关题目
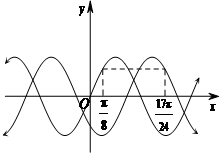 已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )
已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=
如图所示,四边形PDCE为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=