题目内容
17. 已知函数f(x)=x2-2|x|.
已知函数f(x)=x2-2|x|.(1)去绝对值,把函数f(x)写成分段函数的形式,并作出其图象;
(2)求函数f(x)的单调区间;
(3)求函数f(x)的最小值.
分析 (1)去绝对值,得到函数f(x)的解析式,画图即可,
(2)根据图象可得答案,
(3)结合图象,根据函数的单调性可得函数的最小值.
解答 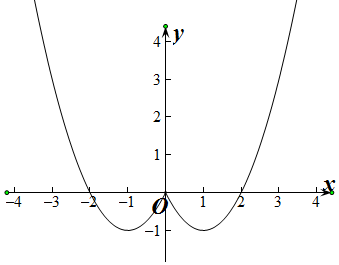 (1)根据题意$f(x)=\left\{\begin{array}{l}{x^2}-2x,x≥0\\{x^2}+2x,x<0\end{array}\right.$,图象如图
(1)根据题意$f(x)=\left\{\begin{array}{l}{x^2}-2x,x≥0\\{x^2}+2x,x<0\end{array}\right.$,图象如图
(2)根据图象,函数的减区间(-∞,-1)、(0,1);函数的增区间[-1,0]、[1,+∞)
(3)当x≥0时,f(x)=x2-x,为二次函数,对称轴为x=1,
则f(x)为[1,+∞)上的增函数,此时f(x)min=f(1)=-1;
当x<0时,f(x)=x2+x,为二次函数,对称轴为x=-1,
则f(x)为[-1,0]上的增函数,此时f(x)min=f(-1)=-1
点评 本题考查了绝对值函数的图象的画法和识别,以及函数的单调性和最值,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
7.已知抛物线C:x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与C的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$,则抛物线C的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
8.612,840,468的最大公约数为( )
| A. | 2 | B. | 4 | C. | 12 | D. | 24 |
5.函数f(x)在(0,+∞)上为增函数,则不等式f(x)>f(8x-16)的解集为( )
| A. | (2,$\frac{16}{7}$) | B. | (-∞,2) | C. | ($\frac{16}{7}$,+∞) | D. | (2,+∞) |