题目内容
6．设集合A={x|-1＜x＜4}，B={x|-5＜x＜$\frac{3}{2}$}，C={x|1-2a＜x＜2a}．若C⊆（A∩B），求实数a的取值范围．分析 先求出A∩B，再根据条件C⊆（A∩B），建立条件关系即可求实数a的取值范围．
解答 解：当C=ϕ时，1-2a≥2a，$a≤\frac{1}{4}$，
当C≠ϕ，$A∩B=\{x|-1＜x＜\frac{3}{2}\}$，且C⊆（A∩B）．
∴$\left\{\begin{array}{l}1-2a＜2a\\ 2a≤\frac{3}{2}\\ 1-2a≥-1\end{array}\right.$，解得：$\frac{1}{4}＜a≤\frac{3}{4}$．
综上实数a的取值范围是$（-∞，\frac{3}{4}]$．
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16．
某校为了解2015年高一年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如表的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．
（1）求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数；
（2）该校2015年高一年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？
某校为了解2015年高一年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如表的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%．（1）求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数；
（2）该校2015年高一年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？
| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数（本） | 128 | m | 80 | 48 |
已知函数f（x）=x2-2|x|．
如图，四边形ABCD为矩形，EA⊥平面ABCD，EF∥AB，AB=2AE=2EF=4．
15．已知全集U={x|x≤5}，集合A={x|-3＜x＜4}，B={x|-5≤x≤3}，则（∁UA）∩B=（ ）
| A． | {x|-5≤x≤-3} | B． | {x|4＜x＜5，或x≤-3} | C． | {x|-5＜x＜-3} | D． | {x|-5＜x＜5} |
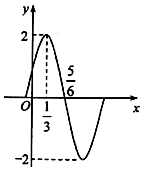函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的图象（部分）如图．