题目内容
8.612,840,468的最大公约数为( )| A. | 2 | B. | 4 | C. | 12 | D. | 24 |
分析 要求三个数的最大公约数,我们可以先求出前两个数的最大公约数,再求出所得公约数与第三个数的最大公约数,即可得到答案.
解答 解:∵840=612+228,612=2×228+156,228=156+72,156=72×2+12,72=6×12
∴612,840的最大公约数是12
同理840,468的最大公约数也为12,
故612,840,468的最大公约数为12,
故选C.
点评 本题考查的知识点是最大公因子,其中在求最大公约数时,要利用辗转相除法,或更相减损术,这是解答本题的关键.

练习册系列答案
相关题目
16. 某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数;
(2)该校2015年高一年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本?
 某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.
某校为了解2015年高一年级学生课外书籍借阅情况,从中随机抽取了40名学生课外书籍借阅情况,将统计结果列出如表的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这40名学生借阅总册数的40%.(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角a的度数;
(2)该校2015年高一年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本?
| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 128 | m | 80 | 48 |
13.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{{x}^{2}+2,x>0}\end{array}\right.$,则f(f(-1))的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.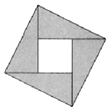 如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )
如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )
 如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )
如图,阴影部分是由四个全等的直角三角形组成的图形,在大正方形内随机取一点,这一点落在小正方形内的概率为 $\frac{1}{5}$,若直角三角形的两条直角边的长分别为a,b(a>b),则$\frac{b}{a}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |

 已知函数f(x)=x2-2|x|.
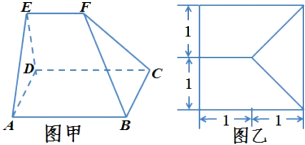
已知函数f(x)=x2-2|x|. 如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.
如图,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=2AE=2EF=4.