题目内容
若曲线y2-xy+2x+k=0过点（a，-a）（a∈R），求k的取值范围．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：由条件可得k=-2a2-2a，再利用二次函数的性质求得它的范围．
解答：
解：由曲线y2-xy+2x+k=0过点（a，-a）（a∈R），可得a2+a2+2a+k=0，
即k=-2a2-2a=-(a+
)2+
≤
，即k的取值范围为（-∞，
]．
即k=-2a2-2a=-(a+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
点评：本题主要考查求二次函数在闭区间上的值域，属于基础题．
练习册系列答案
相关题目
从4名男生和3名女生中选出4人参加迎新座谈会，其中男生甲一定要入选，不同的选法共有 （ ）
| A、120种 | B、24种 |
| C、20种 | D、12种 |
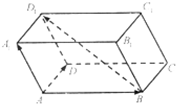如图，四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形，已知| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
运货卡车以每小时x千米（x∈[c，100]，且0＜c＜80）的速度匀速行驶m千米（m为正常数），若汽油的价格是每升7元，而汽车每小时耗油（6+
）升，司机的工资是每小时14元，则这次行车的总费用最低时x的取值为（ ）
| x2 |
| 800 |
| A、c | B、60 | C、80 | D、100 |
某几何体的三视图如图所示，则该几何体的体积为（ ）
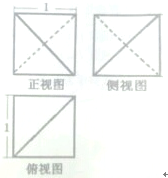
A、
| ||
B、
| ||
C、
| ||
D、
|