题目内容

18．直线$\left\{\begin{array}{l}{x=t-1}\\{y=2-t}\end{array}\right.$（t为参数）与曲线$\left\{\begin{array}{l}{x=3cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数）的交点个数是2．

分析 直线与曲线的参数方程，化为普通方程，联立可得13x2-18x-27=0，即可得出结论．

解答 解：直线$\left\{\begin{array}{l}{x=t-1}\\{y=2-t}\end{array}\right.$（t为参数）与曲线$\left\{\begin{array}{l}{x=3cosθ}\\{y=2sinθ}\end{array}\right.$（θ为参数），普通方程分别为x+y-1=0，$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1，
联立可得13x2-18x-27=0，△=（-18）2-4×13×（-27）＞0，
∴交点个数是2，
故答案为：2．

点评 本题考查直线的参数方程与普通方程的转化，考查方程思想，比较基础．

练习册系列答案
相关题目
8．设a，b，c分别是△ABC三个内角∠A，∠B，∠C的对边，若向量$\overrightarrow m=（{1-cos（A+B），cos\frac{A-B}{2}}）$，$\overrightarrow n=（{\frac{5}{8}，cos\frac{A-B}{2}}）$，且$\overrightarrow m•\overrightarrow n=\frac{9}{8}$．
（1）求tanA•tanB的值；
（2）求$\frac{{2{S_{△ABC}}}}{{{a^2}+{b^2}-{c^2}}}$的最大值．
9．设Tn为数列{an}的前n项之积，即Tn=a1a2a3…an-1an，若${a_1}=2，\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1$，当Tn=11时，n的值为10．
6．如图，已知AC是圆O的直径，PA⊥平面ABCD，E是PC的中点，∠DAC=∠AOB．
（1）证明：BE∥平面PAD
（2）求证：平面BEO⊥平面PCD．
13．已知数列{an}为等比数列，且${a_{2015}}+{a_{2017}}=\int_0^2{\sqrt{4-{x^2}}}dx$，则a2016（a2014+a2018）的最小值为$\frac{{π}^{2}}{2}$．
3．某几何体的三视图如图所示，则其表面积为（　　）
A．6πB．7πC．8πD．12π
10．将函数f（x）=sin2x的图象沿x轴向右平移φ（φ＞0）个单位长度后得到函数g（x）的图象，若函数g（x）的图象关于y轴对称，则当φ取最小的值时，g（0）=-1．
7．在△ABC中，内角A，B，C的对边分别为a，b，c，已知sin2$\frac{B-C}{2}+sinBsinC=\frac{1}{4}$．
（Ⅰ） 求角A的大小；
（Ⅱ） 若b+c=2，求a的取值范围．
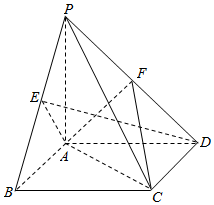8．在四棱锥P-ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，E，F分别是PB，PD的中点．
（Ⅰ）求证：PB∥平面FAC；
（Ⅱ）求三棱锥P-EAD的体积；
（Ⅲ）求证：平面EAD⊥平面FAC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网