题目内容
9.设Tn为数列{an}的前n项之积,即Tn=a1a2a3…an-1an,若${a_1}=2,\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1$,当Tn=11时,n的值为10.分析 由题意可得数列{$\frac{1}{{a}_{n}-1}$}是以$\frac{1}{{a}_{1}-1}=1$为首项,以1为公差的等差数列,求其通项公式,可得数列{an}的通项公式,再由累积法求得Tn,则答案可求.
解答 解:由${a_1}=2,\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n-1}}-1}}=1$,
可得数列{$\frac{1}{{a}_{n}-1}$}是以$\frac{1}{{a}_{1}-1}=1$为首项,以1为公差的等差数列,
则$\frac{1}{{a}_{n}-1}=1+(n-1)×1=n$,
∴${a}_{n}=1+\frac{1}{n}=\frac{n+1}{n}$,
则Tn=a1a2a3…an-1an=$\frac{2}{1}•\frac{3}{2}…\frac{n+1}{n}=n+1$,
由Tn=n+1=11,得n=10.
故答案为:10.
点评 本题考查数列递推式,训练了利用累积法求数列的通项公式,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的体积是( )
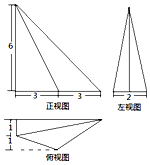

| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
20. 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )
 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
19.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
| A. | $(\;\frac{5}{4}\;,\;6\;)$ | B. | $(\;\frac{5}{3}\;,\;6\;)$ | C. | $(\;\frac{7}{5}\;,\;5\;)$ | D. | $(\;\frac{5}{4}\;,\;5\;)$ |