Question

6．如图，已知AC是圆O的直径，PA⊥平面ABCD，E是PC的中点，∠DAC=∠AOB．
（1）证明：BE∥平面PAD
（2）求证：平面BEO⊥平面PCD．

Answer 1

分析 （1）证明平面OEB∥平面PAD，即可证明BE∥平面PAD；
（2）证明CD⊥平面PAD，利用平面OEB∥平面PAD，证明CD⊥平面OEB，即可证明：平面BEO⊥平面PCD．

解答 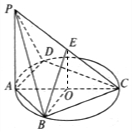证明：（1）连接OE，则OE∥PA，
∵OE?平面PAD，PA?平面PAD，
∴OE∥平面PAD，
∵∠DAC=∠AOB，∴OB∥AD，
∵OB?平面PAD，AD?平面PAD，
∴OB∥平面PAD，
∵OB∩OE=O，
∴平面OEB∥平面PAD，
∵BE?平面OEB，
∴BE∥平面PAD
（2）∵AC是圆O的直径，
∴CD⊥AD，
∵PA⊥平面ABCD，
∴CD⊥PA，
∵PA∩AD=A，
∴CD⊥平面PAD，
∵平面OEB∥平面PAD，
∴CD⊥平面OEB，
∵CD?平面PCD，
∴平面BEO⊥平面PCD．

点评 本题考查线面平行、垂直的证明，考查面面垂直，考查学生分析解决问题的能力属于中档题．