题目内容
设点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,线段AB的中点M恒在圆x2+y2=8内,则点M的横坐标的取值范围为 .
考点:直线与圆相交的性质
专题:直线与圆
分析:设A(x1,y1),B(x2,y2),则3x1-y1-5=0,3x2-y2-13=0,两式相加得3(x1+x2)-(y1+y2)-8=0,设M(x0,y0),则由中点的坐标公式可得3x0-y0-4=0,又点M在圆内,结合点与圆的位置关系即可求出点M的横坐标的取值范围.
解答:
解:设A,B两点的坐标为A(x1,y1),B(x2,y2),
∵点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,
∴3x1-y1-5=0,①
3x2-y2-13=0,②
两式相加得3(x1+x2)-(y1+y2)-8=0.
设线段AB的中点M(x0,y0),
则x1+x2=2x0,y1+y2=2y0.
∴3x0-y0-4=0.
即y0=3x0-4.③
又∵点M恒在圆x2+y2=8内,
∴
+
<8.④
③代入④,得
x02+(3x0-4)2<8.
解得
<x0<2.
∴点M的横坐标的取值范围(
,2).
故答案为:(
,2).
∵点A,B分别在直线3x-y+5=0和3x-y-13=0上运动,
∴3x1-y1-5=0,①
3x2-y2-13=0,②
两式相加得3(x1+x2)-(y1+y2)-8=0.
设线段AB的中点M(x0,y0),
则x1+x2=2x0,y1+y2=2y0.
∴3x0-y0-4=0.
即y0=3x0-4.③
又∵点M恒在圆x2+y2=8内,
∴
| x | 2 0 |
| y | 2 0 |
③代入④,得
x02+(3x0-4)2<8.
解得
| 2 |
| 5 |
∴点M的横坐标的取值范围(
| 2 |
| 5 |
故答案为:(
| 2 |
| 5 |
点评:本题考查点与圆的位置关系,中点的坐标公式以及直线与圆位置关系等知识的综合应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为
从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 定圆O的直径AB=2R,BC为⊙O的动弦,延长BC至D,使CD=BC,AC与OD交于P,求点P轨迹方程.
定圆O的直径AB=2R,BC为⊙O的动弦,延长BC至D,使CD=BC,AC与OD交于P,求点P轨迹方程.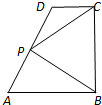 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设