题目内容
某个命题与自然数n有关,如果当n=k(k∈N)时该命题成立,那么可推得当n=k+1时该命题也成立.那么当n= 时,该命题不成立,可推n=5时该命题也不成立.
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:如果当n=k(k∈N)时该命题成立,那么可推得当n=k+1时该命题也成立,利用原命题与其逆否命题的等价性可得答案.
解答:
解:如果当n=k(k∈N)时该命题成立,那么可推得当n=k+1时该命题也成立,
其逆否命题为:当n=k+1时该命题不成立,则当n=k(k∈N)时该命题也不成立.
所以,当n=6时该命题不成立,可推n=5时该命题也不成立,
故答案为:6.
其逆否命题为:当n=k+1时该命题不成立,则当n=k(k∈N)时该命题也不成立.
所以,当n=6时该命题不成立,可推n=5时该命题也不成立,
故答案为:6.
点评:本题考查数学归纳法,熟练应用原命题与其逆否命题的等价性是关键,属于中档题.

练习册系列答案
相关题目
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A、y=
| ||||||||
B、f(x)=
| ||||||||
C、y=
| ||||||||
| D、y=lg|x| |
若点O是△ABC的外心,且
+
+
=
,则△ABC的内角C为( )
| OA |
| OB |
| CO |
| 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为
对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为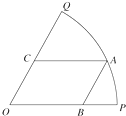 地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=
地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=