题目内容
8.若“?x∈[$\frac{π}{3}$,$\frac{2π}{3}$],cosx≤m”是真命题,则实数m的最小值为( )| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由x的范围求出cosx的范围,然后结合“?x∈[$\frac{π}{3}$,$\frac{2π}{3}$],cosx≤m”是真命题求得m的最小值.
解答 解:当x∈[$\frac{π}{3}$,$\frac{2π}{3}$]时,cosx∈[-$\frac{1}{2}$,$\frac{1}{2}$],
又“?x∈[$\frac{π}{3}$,$\frac{2π}{3}$],cosx≤m”是真命题,
∴m$≥\frac{1}{2}$,即实数m的最小值为$\frac{1}{2}$.
故选:C.
点评 本题考查全程命题,考查了三角函数值域的求法,是基础题.

练习册系列答案
相关题目
18.三棱锥P-ABC中,PA⊥底面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
19.已知集合A={x|x2<1},集合B={x|$\frac{1}{x}$<1},则A∩B=( )
| A. | (-1,0) | B. | (0,1) | C. | (1,+∞) | D. | ∅ |
16.用反证法证明某命题时,对其结论:“自然数a,b,c中恰有一个偶数”正确的反设为( )
| A. | a,b,c都是奇数 | |
| B. | a,b,c中至少有两个偶数或都是奇数 | |
| C. | a,b,c中至少有两个偶数 | |
| D. | a,b,c都是偶数 |
20.函数f(x)=x2-ln|x|的大致图象为( )
| A. | 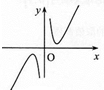 | B. | 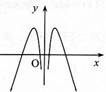 | C. | 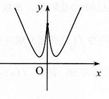 | D. | 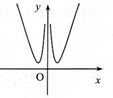 |
18.对于定义在R上的函数f(x),如果存在实数a,使得f(a+x)•f(a-x)=1对任意实数x∈R恒成立,则称f(x)为关于a的“倒函数”.已知定义在R上的函数f(x)是关于0和1的“倒函数”,且当x∈[0,1]时,f(x)的取值范围为[1,2],则当x∈[-2016,2016]时,f(x)的取值范围为( )
| A. | [1,2] | B. | $[\frac{1}{2},2]$ | C. | $[\frac{1}{2},2016]$ | D. | R |
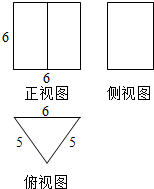 某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.
某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.