题目内容
在△ABC中,角A、B、C对边分别为a、b、c,且2cos(B-C)-1=4cosBcosC.
(Ⅰ)求角A的大小;
(Ⅱ)若a=3,2sinB=sinC,求b,c.
(Ⅰ)求角A的大小;
(Ⅱ)若a=3,2sinB=sinC,求b,c.
考点:正弦定理的应用,两角和与差的余弦函数
专题:计算题,三角函数的求值,解三角形
分析:(Ⅰ)由两角和差的余弦公式,以及诱导公式,即可求得角A;
(Ⅱ)运用余弦定理和正弦定理,解关于b,c的方程,即可得到.
(Ⅱ)运用余弦定理和正弦定理,解关于b,c的方程,即可得到.
解答:
解:(Ⅰ)2cos(B-C)-1=4cosBcosC,
即为2cosBcosC+2sinBsinC-1=4cosBcosC,
2(cosBcosC-sinBsinC)=-1,
即cos(B+C)=-
,即cosA=
,
由于A为三角形的内角,则A=
;
(Ⅱ)由余弦定理可得,a2=b2+c2-2bccosA,
即9=b2+c2-2bccos
,
b2+c2-bc=9,
又2sinB=sinC,由正弦定理可得,2c=b,
解得,b=2
,c=
.
即为2cosBcosC+2sinBsinC-1=4cosBcosC,
2(cosBcosC-sinBsinC)=-1,
即cos(B+C)=-
| 1 |
| 2 |
| 1 |
| 2 |
由于A为三角形的内角,则A=
| π |
| 3 |
(Ⅱ)由余弦定理可得,a2=b2+c2-2bccosA,
即9=b2+c2-2bccos
| π |
| 3 |
b2+c2-bc=9,
又2sinB=sinC,由正弦定理可得,2c=b,
解得,b=2
| 3 |
| 3 |
点评:本题考查正弦定理和余弦定理的运用,考查两角和差的余弦公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知等比数列{an}的前n项和为Sn,且满足
=2,则公比q=( )
| S8 |
| S4 |
| A、±2 | B、±1 | C、-1 | D、1 |
若
,
均为单位向量,且
•
=0,(
-
)•(
-
)≤0,则|2
-
|的最大值为( )
|
| b |
| a |
| b |
| a |
| c |
| b |
| c |
| a |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
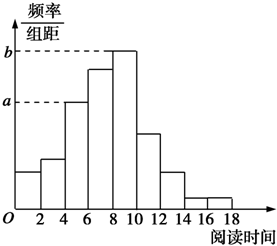 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频率分布表和频率分布直方图: