题目内容
(1+x2)(1-x)8的展开式中,x4的系数是 .
考点:二项式系数的性质
专题:二项式定理
分析:按照二项式定理把(1-x)8展开,可得(1+x2)(1-x)8的展开式中x4的系数.
解答:
解:因为(1+x2)(1-x)8=(1+x2)(1-
•x+
•x2-
•x3+
•x4-…+
•x8 ),
故展开式中x4的系数是
+
=70+28=98,
故答案为:98.
| C | 1 8 |
| C | 2 8 |
| C | 3 8 |
| C | 4 8 |
| C | 8 8 |
故展开式中x4的系数是
| C | 4 8 |
| C | 2 8 |
故答案为:98.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题是真命题的是( )
| A、若m∥n,m∥β,则n∥β |
| B、若m∥β,α⊥β,则m⊥α |
| C、若m∥n,m⊥β,则n⊥β |
| D、若m?α,n?β,α∥β,则m∥n |

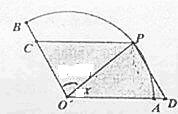 半径为1,圆心角为120°的扇形,点P是扇形AB弧上的动点,设∠POA=x.
半径为1,圆心角为120°的扇形,点P是扇形AB弧上的动点,设∠POA=x.