题目内容
已知复数z=lg(m2-2m-2)+(m2+3m+2)i,根据以下条件分别求实数m的值或范围:
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
考点:复数的代数表示法及其几何意义,复数的基本概念
专题:数系的扩充和复数
分析:(1)由z的实部等于0且虚部不等于0求得m的值;
(2)由z的实部小于0且虚部大于0求解不等式组得答案.
(2)由z的实部小于0且虚部大于0求解不等式组得答案.
解答:
解:(1)由z=lg(m2-2m-2)+(m2+3m+2)i是纯虚数,
得
,即
,解得m=3;
(2)由z对应的点在复平面的第二象限,
得
,即
,解得:2<m<3.
得
|
|
(2)由z对应的点在复平面的第二象限,
得
|
|
点评:本题考查了复数的基本概念,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
已知p:关于x的不等式x2+2ax-a>0的解集是R,q:-1≤a≤0,则p是q的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
若sinα-3cosα=0,则
的值为( )
| sinα+cosα |
| sinα-cosα |
A、-
| ||
| B、2 | ||
| C、-2 | ||
D、
|
设a=log20.3,b=20.3,c=0.32,则下列不等式成立的是( )
| A、c<b<a |
| B、b<a<c |
| C、a<c<b |
| D、c<a<b |
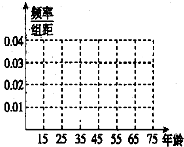 2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表: