题目内容
12.一个几何体的三视图如图所示,则该几何体的体积为( )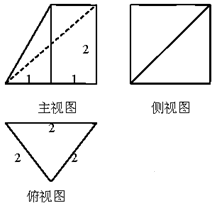
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
分析 由已知可得:该几何体是一个以俯视图为底面的三棱柱,切去一个同底同高的三棱锥所得的几何体,进而得到答案.
解答 解:由已知可得:该几何体是一个以俯视图为底面的三棱柱,
切去一个同底同高的三棱锥所得的几何体,
其底面面积S=$\frac{\sqrt{3}}{4}•{2}^{2}$=$\sqrt{3}$,
高h=2,
故几何体的体积V=Sh-$\frac{1}{3}$Sh=$\frac{{4\sqrt{3}}}{3}$,
故选:C
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.已知集合A={x|x2-2x<0},B={y|y=|x|+1,x∈R},则A∩∁RB=( )
| A. | (0,2) | B. | [1,2) | C. | (0,1] | D. | (0,1) |
7.已知命题p:若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$;命题q:若m>1,则函数 y=x2+mx+1有两个零点.在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,为真命题的是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
1.运行如图所示框图的相应程序,若输入a,b的值分别为log43和log34,则输出M的值是( )

| A. | 0 | B. | 1 | C. | 3 | D. | -1 |
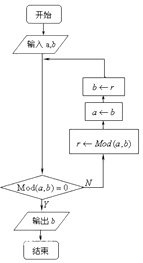 辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.