题目内容

9．若$a={5^{-\frac{1}{2}}}，b={log_2}$3，c=ln2，则（　　）
A．a＜b＜cB．b＜a＜cC．a＜c＜bD．c＜a＜b

分析 利用指数函数与对数函数的运算性质及其单调性即可得出．

解答 解：$a={5^{-\frac{1}{2}}}=\frac{1}{{\sqrt{5}}}＜\frac{1}{2}$，∴$a∈（{0，\frac{1}{2}}）$；
b=log23＞log22=1，∴b∈（1，+∞）；
$\frac{1}{2}=ln\sqrt{e}＜ln2＜lne=1$，∴$c∈（{\frac{1}{2}，1}）$，
于是a＜c＜b．
故选：C．

点评 本题考查了指数函数与对数函数的运算性质及其单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
19．某厂家拟在“五一”节举行大型促销活动，经测算某产品销售价格x（单位：元/件）与每日销售量y（单位：万件）满足关系式y=$\frac{a}{x-2}$+2（x-5）2，其中2＜x＜5，a为常数，已知销售价格为3元时，每日销售量10万件．
（1）求a的值；
（2）若该商品的成本为2元/件，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大．
20．若${2^a}={log_{\frac{1}{2}}}a，{（\frac{1}{2}）^b}={log_2}b，{（\frac{1}{2}）^c}={log_{\frac{1}{2}}}c$，则（　　）
A．a＜b＜cB．b＜a＜cC．a＜c＜bD．c＜a＜b
17．已知函数f（x）=x3+2x2-3的导函数为f′（x），则f′（-2）等于（　　）
A．4B．6C．10D．20
4．已知命题p：?x∈R，x+1≤ex，则￢p（　　）
A．?x∈R，x+1＞exB．?x∈R，x+1≥exC．?x∈R，x+1≥exD．?x∈R，x+1＞ex
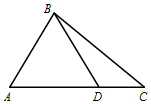14．在△ABC中（图），$A=\frac{π}{3}，cosC=\frac{{2\sqrt{7}}}{7}，BC=\sqrt{7}，\overrightarrow{AD}=2\overrightarrow{DC}$．
（Ⅰ）求边AC的长；
（Ⅱ）求sin∠CBD．
1．已知函数f（x）=lnx-$\frac{1}{2}$ax2+x，a∈R
（1）当a=0时，求函数在（1，f（1）））处的切线方程
（2）令g（x）=f（x）-ax+1，求g（x）的极值．
18．（x2-$\frac{1}{x}$）6的展开式，x6的系数为（　　）
A．15B．6C．-6D．-15
19．已知正项数列{an}是公差为2的等差数列，数列{bn}满足b1=1，b2=$\frac{5}{3}$，且bn+1-bn=$\frac{2}{{a}_{n}{a}_{n+1}}$．
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）设cn=$\frac{1}{（2-{b}_{n}）•{2}^{{a}_{n}}}$，求数列{cn}的前n项和Tn，并证明$\frac{1}{2}$≤Tn＜$\frac{10}{9}$对一切n∈N*都成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网