题目内容
求下列各函数的导函数:
(1)f(x)=kx+
;
(2)f(x)=k
+l
;
(3)f(x)=
+
.
(1)f(x)=kx+
| ax2+bx+c |
(2)f(x)=k
| ax+b |
| cx+d |
(3)f(x)=
| (x-a)2+b2 |
| (x-c)2+d2 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则和复合函数的求导法则,计算即可.
解答:
解:1)f′(x)=kx+
=k+
•(2a+b)=k+
.
(2)f′(x)=k
+l
=
•(ax+b)-
+
•(cx+d)-
(3)f′(x)=
+
=(x-a)•[(x-a)2+b2]-
+(x-c)•[(x-c)2+d2)-
| ax2+bx+c |
| 1 |
| 2 |
| 1 | ||
|
(2a+b)
| ||
| 2(ax2+bx+c) |
(2)f′(x)=k
| ax+b |
| cx+d |
| ka |
| 2 |
| 1 |
| 2 |
| lc |
| 2 |
| 1 |
| 2 |
(3)f′(x)=
| (x-a)2+b2 |
| (x-c)2+d2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了导数的运算法则和复合函数的求导法则,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)是R上的奇函数,且在R上有f′(x)>0,则f(1)的值 ( )
| A、恒为正数 | B、恒为负数 |
| C、恒为0 | D、可正可负 |
 某装修公司根据客户要求装饰一个墙角,施工设计时,在墙面交线AB与天花板ACD之间拉一条“定位线”EF(如图),已知墙面交线AB、AC、AD两两垂直,且AB=2,AC=AD=3.(单位:分米)
某装修公司根据客户要求装饰一个墙角,施工设计时,在墙面交线AB与天花板ACD之间拉一条“定位线”EF(如图),已知墙面交线AB、AC、AD两两垂直,且AB=2,AC=AD=3.(单位:分米)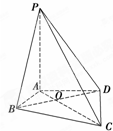 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点. 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
如图所示,有三根针和套在一根针上若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.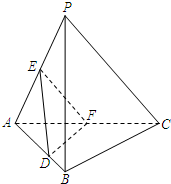 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: