题目内容
复数z满足（z-i）（2-i）=5，则复数z在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数的代数表示法及其几何意义
专题：计算题,数系的扩充和复数
分析：求出z并化简可得z对应点的坐标，由坐标可得答案．
解答：
解：∵（z-i）（2-i）=5，
∴z=
+i=
+i=2+2i，
∴z在复平面内对应的点为（2，2）位于第一象限，
故选A．
∴z=
| 5 |
| 2-i |
| 5(2+i) |
| (2-i)(2+i) |
∴z在复平面内对应的点为（2，2）位于第一象限，
故选A．
点评：该题考查复数代数形式的乘除运算、复数的几何意义，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知球O的表面积为16π，球心O在大小为
的二面角α-l-β的内部，且平面α与球O相切与点M，平面β截球O所得的小圆O′的半径为1（O′为小圆圆心），若点P为圆O上任意一点，记∠MOP为θ，则下列结论正确的是（ ）
| π |
| 3 |
A、当θ取得最小值时，O′P与OM所成角为
| ||
B、当θ取得最小值时，点P到平面α的距离为
| ||
C、θ的最大值为
| ||
| D、θ的最大值为π |
已知随机变量X服从正态分布N（1，4），且P（0≤X≤2）=0.68，则P（X＞2）=（ ）
| A、0.34 | B、0.16 |
| C、0.84 | D、0.32 |
定义在R上的函数f（x）不是常数函数，且满足对任意的x有f（x-1）=f（x+1），f（2-x）=f（x），下列5个结论：
①f（x）是单调函数，
②f（x）的图象关于x=1对称，
③f（x）是周期函数，
④f（x）是偶函数，
⑤f（x）有最大值和最小值．
其中真命题是（ ）
①f（x）是单调函数，
②f（x）的图象关于x=1对称，
③f（x）是周期函数，
④f（x）是偶函数，
⑤f（x）有最大值和最小值．
其中真命题是（ ）
| A、②③④ | B、②③⑤ |
| C、①②⑤ | D、①②③ |
已知函数f（x）是R上的奇函数，且在R上有f′（x）＞0，则f（1）的值 （ ）
| A、恒为正数 | B、恒为负数 |
| C、恒为0 | D、可正可负 |
等差数列{an}中，已知a5+a7=10，Sn是{an}的前n项和，S11等于（ ）
| A、45 | B、50 | C、55 | D、60 |
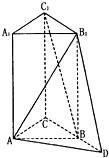已知正三棱柱ABC-A1B1C1中，AA1=2AC=4，延长CB至D，使CB=BD．
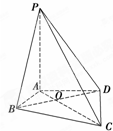如图，在四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=∠ADC=90°，∠BAD=120°，AD=AB=1，AC交BD于O点．