题目内容
8.已知圆O:x2+y2=9,点A(2,0),点P为动点,以线段AP为直径的圆内切于圆O,则动点P的轨迹方程是$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.分析 设AP的中点为M,切点为N,连OM,MN,通过|OM|+|MN|=|ON|=3,推出|OM|+|MN|=3.说明点P的轨迹是以A′,A为焦点,长轴长为6的椭圆.然后求解动点P的轨迹方程.
解答 解:设AP的中点为M,切点为N,连OM,MN,则|OM|+|MN|=|ON|=3,
取A关于y轴的对称点A′,连A′P,
故|A′P|+|AP|=2(|OM|+|MN|)=6.
所以点P的轨迹是以A′,A为焦点,长轴长为6的椭圆.
其中,a=3,c=2,b=$\sqrt{5}$,则动点P的轨迹方程是$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.
故答案为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.
点评 本题考查轨迹方程的求法,判断轨迹的椭圆简化解题的过程,考查直线与椭圆的位置关系的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
19.先后掷骰子两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x+y为偶数”,事件B为“x≠y”,则概率P(B|A)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
18.在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b,若△ABC的面积为S=$\frac{{\sqrt{3}}}{12}$c,则ab的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 3 |
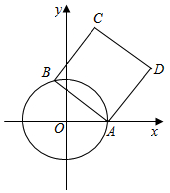 已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.
已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.