题目内容
3.若圆C的方程为(x-3)2+(y-1)2=9与直线斜率为1的直线m交于A,B两点,且以AB为直径的圆过原点,(1)求直线m的方程;
(2)若过点T(1,3)的直线l与圆C交于P,Q两点,线段PQ的中点为M,求M的轨迹方程.
分析 (1)利用圆系知识设出圆的方程,利用以AB为直径的圆过原点,即可求直线m的方程;
(2)设出线段PQ的中点M的坐标,利用圆的圆心与弦垂直,通过斜率乘积为-1,即可求出M的轨迹方程.
解答 解:(1)设直线m的方程为y=x+b,即x-y+b=0,则
与圆C相交于直线m的圆的方程为(x-3)2+(y-1)2-9+λ(x-y+b)=0,圆心为($\frac{6-λ}{2}$,$\frac{2+λ}{2}$)
∵以AB为直径的圆过原点,
∴(0-3)2+(0-1)2-9+λb=0,$\frac{6-λ}{2}$-$\frac{2+λ}{2}$+b=0,
∴b=-1,
∴直线m的方程为y=x-1;
(2)设M(x,y)由题意可知MC⊥MT,
∵C(3,1),T(1,3)
∴$\frac{y-3}{x-1}•\frac{y-1}{x-3}$=-1
整理得(x-2)2+(y-2)2=2,
线段PQ的中点M的轨迹方程:x-2)2+(y-2)2=2.
点评 本题考查直线与圆的位置关系,考查圆系知识,考查直线的垂直关系的应用,考查计算能力,转化思想.

练习册系列答案
相关题目
14.曲线$\left\{\begin{array}{l}{x=|sinθ|}\\{y=cosθ}\end{array}\right.$(θ为参数)的方程等价于( )
| A. | x=$\sqrt{1-{y}^{2}}$ | B. | y=$\sqrt{1-{x}^{2}}$ | C. | y=±$\sqrt{1-{x}^{2}}$ | D. | x2+y2=1 |
11.记等式1•n+2•(n-1)+3•(n-2)+…+n•1=$\frac{1}{6}$n(n+1)(n+2)左边的式子为f(n),用数学归纳法证明该等式的第二步归纳递推时,即当n从k变为k+1时,等式左边的改变量f(k+1)-f(k)=( )
| A. | k+1 | B. | 1•(k+1)+(k+1)•1 | C. | 1+2+3+…+k | D. | 1+2+3+…+k+(k+1) |
12.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示.
请根据以上数据分析,这个经营部定价在11.5元/桶才能获得最大利润.
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
13.已知(1-2x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a3+a4等于( )
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
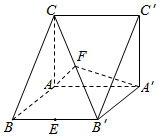 在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,
在三棱ABC-A′B′C′中,侧棱AA′⊥底面ABC,AC⊥AB,AB=2,AC=AA′=3,