题目内容
8.若(x-1)5+x10=a0+a1(1+x)+a2(1+x)2+…+a10(1+x)10,则a3的值是-80.分析 由等式的右侧发现a3的值是(1+x)3的系数,所以只要将等式左边转化为关于x+1的二项式,然后求系数即可.
解答 解:由等式的右侧发现a3的值是(1+x)3的系数,
所以(x-1)5+x10=[(x+1)-2]5+[(x+1)-1]10,
展开式中(x+1)3的项为${C}_{5}^{2}(x+1)^{3}(-2)^{2}+{C}_{10}^{7}(x+1)^{3}(-1)^{7}$=-80(x+1)3.
所以a3的值是-80;
故答案为:-80.
点评 本题考查了二项展开式的系数的求法;本题的关键是将等式左边转化为关于(x+1)的二项式,然后求特征项.

练习册系列答案
相关题目
19.在△ABC中,$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{8}{5}$,则△ABC的形状为( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
10.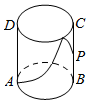 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )| A. | $\sqrt{5}$ | B. | π+1 | C. | $\sqrt{{π}^{2}+1}$ | D. | $\sqrt{{π}^{2}+9}$ |

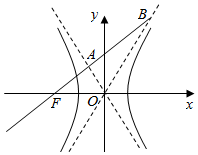 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$. 已知正六棱柱的底面边长为2,侧棱长为3,其三视图中的俯视图如图所示,则其左视图的面积是6$\sqrt{3}$.
已知正六棱柱的底面边长为2,侧棱长为3,其三视图中的俯视图如图所示,则其左视图的面积是6$\sqrt{3}$.