题目内容
20.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2$\sqrt{2}$,其上下顶点分别为C1,C2,点A(1,0),B(3,2),AC1⊥AC2.(1)求椭圆E的方程及离心率;
(2)点P的坐标为(m,n)(m≠3),过点A任意作直线l与椭圆E相交于点M,N两点,设直线MB,BP,NB的斜率依次成等差数列,探究m,n之间是否满足某种数量关系,若是,请给出m,n的关系式,并证明;若不是,请说明理由.
分析 (1)由AC1⊥AC2,可得$\overrightarrow{A{C}_{1}}$•$\overrightarrow{A{C}_{2}}$=1-b2=0,又2c=2$\sqrt{2}$,a2=b2+c2,即可得出.
(2)m,n之间满足数量关系m=n+1.下面给出证明:①当取M$(\sqrt{3},0)$,N$(-\sqrt{3},0)$时,根据斜率计算公式、及其直线MB,BP,NB的斜率依次成等差数列即可证明.
②当直线MN的斜率不为0时,设直线MN的方程为:ty+1=x.M(x1,y1),N(x2,y2).与椭圆方程联立化为:(t2+3)y2+2ty-2=0,根据斜率计算公式、及其直线MB,BP,NB的斜率依次成等差数列、根与系数的关系化简即可证明.
解答 解:(1)∵AC1⊥AC2,C1(0,b),C2(0,-b),A(1,0),
∴$\overrightarrow{A{C}_{1}}$•$\overrightarrow{A{C}_{2}}$=1-b2=0,∴b2=1.
∵2c=2$\sqrt{2}$,解得c=$\sqrt{2}$,∴a2=b2+c2=3.
∴椭圆E的方程为$\frac{{x}^{2}}{3}+{y}^{2}$=1.
离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$.
(2)m,n之间满足数量关系m=n+1.下面给出证明:
①当取M$(\sqrt{3},0)$,N$(-\sqrt{3},0)$时,kMB=$\frac{2}{3-\sqrt{3}}$,kBP=$\frac{2-n}{3-m}$,kNB=$\frac{2}{3+\sqrt{3}}$,
∵直线MB,BP,NB的斜率依次成等差数列,∴2×$\frac{2-n}{3-m}$=$\frac{2}{3-\sqrt{3}}$+$\frac{2}{3+\sqrt{3}}$,化为:m=n+1.
②当直线MN的斜率不为0时,设直线MN的方程为:ty+1=x.M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}{ty+1=x}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,化为:(t2+3)y2+2ty-2=0,
∴y1+y2=$\frac{-2t}{{t}^{2}+3}$,y1y2=$\frac{-2}{{t}^{2}+3}$.
kMB=$\frac{{y}_{1}-2}{{x}_{1}-3}$,kBP=$\frac{2-n}{3-m}$,kNB=$\frac{{y}_{2}-2}{{x}_{2}-3}$,
∵直线MB,BP,NB的斜率依次成等差数列,
∴2×$\frac{2-n}{3-m}$=$\frac{{y}_{1}-2}{{x}_{1}-3}$+$\frac{{y}_{2}-2}{{x}_{2}-3}$,
由于$\frac{{y}_{1}-2}{{x}_{1}-3}$+$\frac{{y}_{2}-2}{{x}_{2}-3}$=$\frac{({y}_{1}-2)(t{y}_{2}-2)+({y}_{2}-2)(t{y}_{1}-2)}{(t{y}_{1}-2)(t{y}_{2}-2)}$=$\frac{2t{y}_{1}{y}_{2}-(2t+2)({y}_{1}+{y}_{2})+8}{{t}^{2}{y}_{1}{y}_{2}-2t({y}_{1}+{y}_{2})+4}$=2,
∴$\frac{2-n}{3-m}$=1,化为:m=n+1.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式、等差数列的性质,考查了推理能力与计算能力,属于难题.

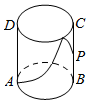 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )| A. | $\sqrt{5}$ | B. | π+1 | C. | $\sqrt{{π}^{2}+1}$ | D. | $\sqrt{{π}^{2}+9}$ |
| A. | k+1 | B. | 1•(k+1)+(k+1)•1 | C. | 1+2+3+…+k | D. | 1+2+3+…+k+(k+1) |
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
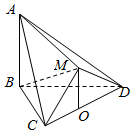 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.