题目内容
18.在△ABC中,角A,B,C的对边分别为a,b,c,且2ccosB=2a+b,若△ABC的面积为S=$\frac{{\sqrt{3}}}{12}$c,则ab的最小值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 3 |
分析 由正弦定理将2ccosB=2a+b,转化成2sinC•cosB=2sin A+sinB,由三角形内角和定理,将sin A=sin(B+C),利用两角和的正弦公式展开,化简求得,
sinC的值,由余弦定理、三角形的面积公式及基本不等式关系,求得ab的最小值.
解答 解:由正弦定理,有$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,又2c•cosB=2a+b,得
2sinC•cosB=2sin A+sinB,
由A+B+C=π,得sin A=sin(B+C),
则2sinC•cosB=2sin(B+C)+sinB,即2sinB•cosC+sinB=0,
又0<B<π,sinB>0,得cosC=-$\frac{1}{2}$,
因为0<C<π,得C=$\frac{2π}{3}$,
则△ABC的面积为S△=$\frac{1}{2}$ab sinC=$\frac{\sqrt{3}}{4}$ab,即c=3ab,
由余弦定理,得c2=a2+b2-2ab cosC,化简,得a2+b2+ab=9a2b2,
∵a2+b2≥2ab,当仅当a=b时取等号,
∴2ab+ab≤9a2b2,即ab≥$\frac{1}{3}$,故ab的最小值是$\frac{1}{3}$.
故答案选:B.
点评 本题考查正余弦定理、三角形内角和定理及基本不等式相结合,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.某空调专卖店试销A、B、C三种新型空调,销售情况如表所示:
(1)求A型空调前三周的平均周销售量;
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
13.已知(1-2x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a3+a4等于( )
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
6.从抛物线y2=4x的准线l上一点P引抛物线的两条切线PA,PB,A,B为切点,若直线AB的倾斜角为$\frac{π}{3}$,则P点的纵坐标为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |

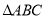 和
和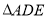 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点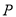 为射线
为射线 与射线
与射线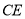 的交点.
的交点.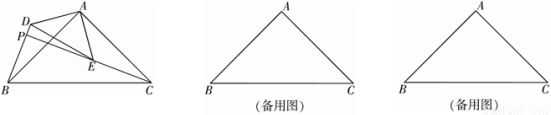
 ;
; ,把
,把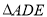 绕点
绕点 旋转,
旋转, 时,求
时,求 的长;
的长;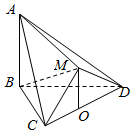 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.