题目内容
17.设P是曲线2x2-y2=1上的一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程为8x2-4y2=1.分析 设P(x,y),M(x0,y0),根据中点坐标公式,利用代入法进行化简即可.
解答 解:设P(x,y),M(x0,y0),因为M是线段OP的中点,
则有$\left\{\begin{array}{l}{x_0}=\frac{x}{2}\\{y_0}=\frac{y}{2}\end{array}\right.⇒\left\{\begin{array}{l}x=2{x_0}\\ y=2{y_0}\end{array}\right.$,
所以$2×{(2{x_0})^2}-{({y_0})^2}=1$,即$8x_0^2-y_0^2=1$,
故答案为8x2-4y2=1.
点评 本题主要考查点的轨迹方程的求解,设出点的坐标,根据中点坐标关系,利用代入法是解决本题的关键.难度不大.

练习册系列答案
相关题目
12.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示.
请根据以上数据分析,这个经营部定价在11.5元/桶才能获得最大利润.
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
9.某空调专卖店试销A、B、C三种新型空调,销售情况如表所示:
(1)求A型空调前三周的平均周销售量;
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量(台) | 11 | 10 | 15 | A4 | A5 |
| B型数量(台) | 9 | 12 | 13 | B4 | B5 |
| C型数量(台) | 15 | 8 | 12 | C4 | C5 |
(2)为跟踪调查空调的使用情况,根据销售记录,从前三周售出的所有空调中随机抽取一台,求抽到的空调不是B型且不是第一周售出空调的概率;
(3)根据C型空调前三周的销售情况,预估C型空调五周的平均周销售量为10台,当C型空调周销售量的方差最小时,求C4,C5的值.
(注:方差s2=$\frac{1}{n}$[(x${\;}_{1}-\overline{x}$)2+(x${\;}_{2}-\overline{x}$)2+…+(xn-$\overline{x}$)2],其中$\overline{x}$为x1,x2,…,xn的平均数)
 已知正六棱柱的底面边长为2,侧棱长为3,其三视图中的俯视图如图所示,则其左视图的面积是6$\sqrt{3}$.
已知正六棱柱的底面边长为2,侧棱长为3,其三视图中的俯视图如图所示,则其左视图的面积是6$\sqrt{3}$.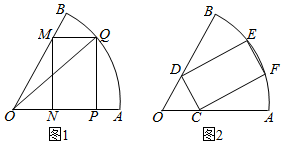 如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.
如图,在中心角为60°,半径为1的扇形OAB的半径OB上任取一点M,作内接矩形MNPQ,设∠QOA=θ,矩形MNPQ的面积为S.