题目内容
若角θ的终边过点P(-4a,3a)(a≠0),
(Ⅰ)求sinθ+cosθ的值
(Ⅱ)试判断cos(sinθ)•sin(cosθ)的符号.
(Ⅰ)求sinθ+cosθ的值
(Ⅱ)试判断cos(sinθ)•sin(cosθ)的符号.
考点:任意角的三角函数的定义,三角函数值的符号
专题:计算题,三角函数的求值
分析:(Ⅰ)由题意可得 x=-4a,y=3a,r=5|a|,再分类讨论,利用任意角的三角函数的定义进行运算,可得答案;
(Ⅱ)分类讨论,确定sinθ、cosθ的取值,即可得出结论.
(Ⅱ)分类讨论,确定sinθ、cosθ的取值,即可得出结论.
解答:
解:(Ⅰ)∵角θ的终边过点P(-4a,3a)(a≠0),
∴x=-4a,y=3a,r=5|a|.
当a>0时,r=5a,sinθ+cosθ=
.
当a<0时,r=-5a,sinθ+cosθ=-
.
(Ⅱ)当a>0时,sinθ=
∈(0,
),cosθ=-
∈(-
,0),
则cos(sinθ)•sin(cosθ)=cos
•sin(-
)<0;
当a<0时,sinθ=-
∈(-
,0),cosθ=-
∈(0,
),
则cos(sinθ)•sin(cosθ)=cos(-
)•sin
>0.
∴x=-4a,y=3a,r=5|a|.
当a>0时,r=5a,sinθ+cosθ=
| 1 |
| 5 |
当a<0时,r=-5a,sinθ+cosθ=-
| 1 |
| 5 |
(Ⅱ)当a>0时,sinθ=
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
| π |
| 2 |
则cos(sinθ)•sin(cosθ)=cos
| 3 |
| 5 |
| 4 |
| 5 |
当a<0时,sinθ=-
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
| π |
| 2 |
则cos(sinθ)•sin(cosθ)=cos(-
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题考查任意角的三角函数的定义,两点间的距离公式的应用,体现了分类讨论的数学思想.求出r值,是解题的关键.

练习册系列答案
相关题目
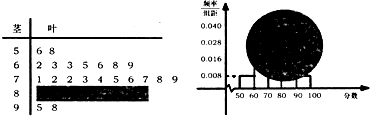 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题: 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.