题目内容
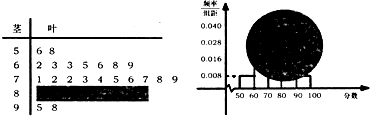 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:(Ⅰ)求本次测试成绩的中位数,并求频率分布直方图中[80,90)的矩形的高(用小数表示);
(Ⅱ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
考点:频率分布直方图,频率分布表,古典概型及其概率计算公式
专题:概率与统计
分析:(I)根据分数在[50,60)的频数为2,频率为0.008×10=0.08,可计算出样本容量,进而得到中位数,结合各组累积频数等于样本容量,可求出分数在[80,90)的频数,进而求出分数在[80,90)的频率,进而求出分数在[80,90)的矩形的高.
(II)将[80,90)之间的4份试卷记为a,b,c,d,[90,100]之间的2份试卷记为1,2.求出从中任取两个学生的基本事件总数和满足至少有一份分数在[90,100]之间的基本事件个数,代入古典概型概率计算公式,可得答案.
(II)将[80,90)之间的4份试卷记为a,b,c,d,[90,100]之间的2份试卷记为1,2.求出从中任取两个学生的基本事件总数和满足至少有一份分数在[90,100]之间的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(Ⅰ)由茎叶图知,分数在[50,60)的频数为2,频率为0.008×10=0.08,
∴全班人数为
=25,
∴本次测试成绩的中位数为73,
由茎叶图知,分数在[80,90)的频数为25-2-7-10-2=4,
频率分布直方图中[80,90)的矩形的高为
÷10=0.016,
(Ⅱ)将[80,90)之间的4份试卷记为a,b,c,d,[90,100]之间的2份试卷记为1,2.
在[80,100]之间任取两份试卷的基本事件为:
(a,b),(a,c),(a,d),(a,1),(a,2),
(b,c),(b,d),(b,1),(b,2),(c,d),
(c,1),(c,2),(d,1),(d,2),(1,2)共15个,
其中至少有一个在[90,100]之间的基本事件有:
(a,1),(a,2),(b,1),(b,2),(c,1),
(c,2),(d,1),(d,2),(1,2)共9个,
∴至少有一份分数在[90,100]之间的概率为
=
.
∴全班人数为
| 2 |
| 0.08 |
∴本次测试成绩的中位数为73,
由茎叶图知,分数在[80,90)的频数为25-2-7-10-2=4,
频率分布直方图中[80,90)的矩形的高为
| 4 |
| 25 |
(Ⅱ)将[80,90)之间的4份试卷记为a,b,c,d,[90,100]之间的2份试卷记为1,2.
在[80,100]之间任取两份试卷的基本事件为:
(a,b),(a,c),(a,d),(a,1),(a,2),
(b,c),(b,d),(b,1),(b,2),(c,d),
(c,1),(c,2),(d,1),(d,2),(1,2)共15个,
其中至少有一个在[90,100]之间的基本事件有:
(a,1),(a,2),(b,1),(b,2),(c,1),
(c,2),(d,1),(d,2),(1,2)共9个,
∴至少有一份分数在[90,100]之间的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知tan(π-a)=2,则
=( )
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
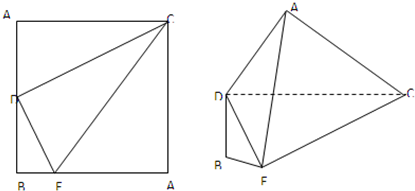 如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC.
如图,正方形A1BA2C的边长为4,D是A1B的中点,E是BA2上的点,将△A1DC及△A2EC分别沿DC和EC折起,使A1、A2重合于A,且平面ADC⊥平面EAC. 如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°
如图,已知三棱锥V-ABC中,VA⊥平面ABC,且AC=2,VA=2,∠ABC=90°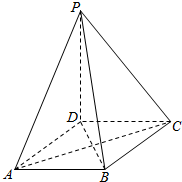 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.