题目内容
（1）已知向量
=（sinθ，-2）与
=（1，cosθ）互相垂直，其中θ∈（0，
）．求sinθ和cosθ的值；
（2）已知非零向量
，
满足|
|=1，（
-
）•（
+
）=
，且
•
=
．求向量
-
的模．
| a |
| b |
| π |
| 2 |
（2）已知非零向量
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）根据向量
=（sinθ，-2）与
=（1，cosθ）互相垂直，可得
•
=sin θ-2cos θ=0，再自用平方关系式求出sinθ和cosθ的值；
（2）先求向量
-
的模的平方，然后再开方求模长．
| a |
| b |
| a |
| b |
（2）先求向量
| a |
| b |
解答：
解：（1）∵
⊥
，∴
•
=sin θ-2cosθ=0，
即sinθ=2cosθ．又∵sin2θ+cos2θ=1，
∴4cos2θ+cos2θ=1，即cos2θ=
，
∴sin2θ=
．又θ∈（0，
），
∴sin θ=
，cos θ=
．…（7分）
（2）|
-
|2=（
-
）2
=|
|2-2|
||
|cos θ+|
|2=
，
∴|
-
|=
..…（14分）
| a |
| b |
| a |
| b |
即sinθ=2cosθ．又∵sin2θ+cos2θ=1，
∴4cos2θ+cos2θ=1，即cos2θ=
| 1 |
| 5 |
∴sin2θ=
| 4 |
| 5 |
| π |
| 2 |
∴sin θ=
2
| ||
| 5 |
| ||
| 5 |
（2）|
| a |
| b |
| a |
| b |
=|
| a |
| a |
| b |
| b |
| 1 |
| 2 |
∴|
| a |
| b |
| ||
| 2 |
点评：本题考查了向量的数量积及模长，数量积有两种运算方式，一种是坐标运算，一种是几何运算，根据题设选择适当的形式进行运算．
练习册系列答案
相关题目
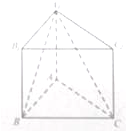如图，在直三棱柱ABC-A1B1C1中，AB=2，AC=AA1=2
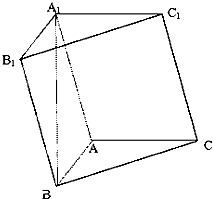在三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=A1B=2，顶点A1在底面ABC上的射影恰好为点B．
如图，在半径为2