题目内容
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.(Ⅰ)证明:DE⊥SC
(Ⅱ)求四棱锥E-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)DE⊥SC?DE⊥面SBC?
?
?
,以下由已知易证;
(2)由(1)DE是Rt△SBD的高,而SD、BD容易求得,底面ABCD是直角梯形,各边长都已知,因此面积可求,代入公式可求得四棱锥E-ABCD的体积.
|
|
|
(2)由(1)DE是Rt△SBD的高,而SD、BD容易求得,底面ABCD是直角梯形,各边长都已知,因此面积可求,代入公式可求得四棱锥E-ABCD的体积.
解答:
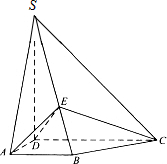 解:(1)证明:连接BD,过B作BF⊥CE,垂足为F.
解:(1)证明:连接BD,过B作BF⊥CE,垂足为F.
因为平面EDC⊥平面SBC.平面EDC∩平面SBC=EC
BF?面SBC,BF⊥EC,
所以,BF⊥面DEC,所以DE⊥BF,
由题意得:BC⊥BD,BC⊥SD,SD∩BD=D,
所以BC⊥面SBD,又因为DE?面SBD,
所以DE⊥BC,
BC∩BF=B,所以DE⊥面SBC,
所以DE⊥SC.
(2)由(1)知DE⊥SB,SD=2,BD=
∴SB=
,
∴DE=
,∴在Rt△BDE中BD=
=
,
∴SE:EB=2:1,
∴E到面ABCD的距离为
SD=
,
∴VE-ABCD=
(
×3×1)
=
.
 解:(1)证明:连接BD,过B作BF⊥CE,垂足为F.
解:(1)证明:连接BD,过B作BF⊥CE,垂足为F.因为平面EDC⊥平面SBC.平面EDC∩平面SBC=EC
BF?面SBC,BF⊥EC,
所以,BF⊥面DEC,所以DE⊥BF,
由题意得:BC⊥BD,BC⊥SD,SD∩BD=D,
所以BC⊥面SBD,又因为DE?面SBD,
所以DE⊥BC,
BC∩BF=B,所以DE⊥面SBC,
所以DE⊥SC.
(2)由(1)知DE⊥SB,SD=2,BD=
| 2 |
| 6 |
∴DE=
| 2 | ||
|
| BD2-DE2 |
| ||
| 3 |
∴SE:EB=2:1,
∴E到面ABCD的距离为
| 1 |
| 3 |
| 2 |
| 3 |
∴VE-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题第一问的关键是把底面梯形研究清楚,然后根据线线垂直的证明思路寻找条件;而体积的计算问题难点在于选好底面(面积好求),选好高(最好是在一个直角三角形中),而此直角三角形又可以解,三棱锥的体积计算问题为达以上目的常常采用变换顶点的方法解决问题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
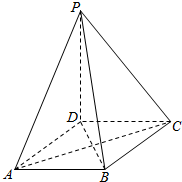 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,. 如图,在半径为2
如图,在半径为2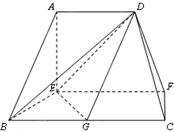 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.